Даны уравнения 7x+4y=4 и x−y=0. На какие числа нужно умножить эти уравнения, чтобы при их сложении в левой части коэффициент при x был равен 1, а коэффициент при y был равен 0?
Первое уравнение нужно умножить на :
, второе — на :
.

1.Вычислите: а)180*94-47700:45+4946
б)86*170-5793+72800:35
2.Длина прямоугольного участка земли 125 м, а ширина 96 м. Найдите площадь поля и выразите её в арах.
3.Найдите объём прямоугольного параллелепипеда, измерения которого равны 4м, 3м и 5м.
4.Используя формулу пути S=V/t,найдите:
а) путь, пройденный автомашиной за 3ч, если её скорость 80км/ч;
б) время движения катера км со скоростью 15км/ч.
5.Найдите площадь поверхности и объём куба, ребро которого равно 6дм. Во сколько раз уменьшится площадь поверхности и во сколько раз – объём куба, если его ребро уменьшить вдвое?
6.Периметр квадрата 48см. Найдите площадь квадрата
7. 10гектаров равны:
а)10000м.кв.
б)100000м.кв.
в)1000000м.кв.
8.Площадь волейбольной площадке 400000см.кв. Длина равна
 а) 500мм;
 б) 50см;
в) 5м.

Свойства степеней(≈7 класс):

Упростите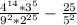

Квадратное уравнение(≈8 класс):

x² – 46x + 529 = 0

С использованием производной(≈11 класс):

y(x) = x⁴ + x³ - 5x² - x + 17

y'(2) = ?

↓↓↓↓↓

Свойства степеней(решение):

Квадратное уравнение(решение):

x² – 46x + 529 = 0

D = b² - 4ac = (-46)² - 4 * 1 * 529 = 2116 - 2116 = 0 => один корень

x = -b/2a = -(-46)/2 = 46/2 = 23

С использованием производной(решение):

y(x) = x⁴ + x³ - 5x² - x + 17

y'(2) = ?

y'(x) = (x⁴)' + (x³)' - (5x²)' - (x)' + (17)' = 4x³ + 3x² - 10x - 1

y'(2) = 4*2³ + 3*2² - 10*2 - 1 = 4*8 + 3*4 - 20 - 1 = 32 + 12 - 21 = 44 - 21 = 23