Даны вершины треугольника авс: "а(" x_1 "; " y_1 ")" , "b(" x_2 "; " y_2 ")" , "c(" x_3 "; " y_3 ")" . найти: а) уравнение стороны ав; б) уравнение высоты сн; в)уравнение медианы am; г) точку n пересечения медианы аm и высоты сн; д) уравнение прямой, проходящей через вершину с, параллельно стороне ав; е) расстояние от точки с до прямой ав. a(-2,4), b(-2,4),c(-2,4); a(-3,-2), b(14,4),c(6,8); a(1,7), b(-3,-1), c(11,-3); a(1,0), b(-1,4), c(9,5); a(1,-2), b(7,1), c(3,7); a(-2,-3), b(1,6), c(6,1); a(-4,2), b(-6,6), c(6,2); a(4,-3), b(7,3), c(1,10); a(4,-4), b(8,2), c(3,8); a(-3,-3), b(5,-7), c(7,7); a(1,-6), b(3,4), c(-3,3); a(-4,2), b(8,-6), c(2,6); a(-5,2), b(0,-4), c(5,7); a(4,-4), b(6,2), c(-1,8); a(-3,8), b(-6,2), c(0,-5); a(6,-9), b(10,-1), c(-4,1); a(4,1), b(-3,-1), c(7,-3); a(-4,2), b(6,-4), c(4,10); a(3,-1), b(11,3), c(-6,2); a(-7,-2), b(-7,4), c(5,-5); a(-1,-4), b(9,6), c(-5,4); a(10,-2), b(4,-5), c(-3,1); a(-3,-1), b(-4,-5), c(8,1); a(-2,-6), b(-3,5), c(4,0); a(-7,-2), b(3,-8), c(-4,6); a(0,2), b(-7,-4), c(3,2); a(7,0), b(1,4), c(-8,-4); a(1,-3), b(0,7), c(-2,4); a(-5,1), b(8,-2), c(1,4); a(2,5), b(-3,1), c(0,4).

2sin x - 4cos x - sin x/cos x - cos x/sin x + 2cos^2 x/sin x + 2 = 0

Умножаем все на sin x*cos x

2sin^2 x*cos x - 4cos^2 x*sin x - sin^2 x - cos^2 x + 2cos^3 x + 2sin x*cos x = 0

2sin x*cos x*(sin x - cos x) - 2sin x*cos^2 x + 2cos^3 x =

= sin^2 x + cos^2 x - 2sin x*cos x

2sin x*cos x*(sin x - cos x) + 2cos^2 x*(cos x - sin x) = (sin x - cos x)^2

(sin x - cos x)*(2sin x*cos x - 2cos^2 x) = (sin x - cos x)^2

2cos x* (sin x - cos x)* (sin x - cos x) = (sin x - cos x)^2

(sin x - cos x)^2*(2cos x - 1) = 0

1) sin x = cos x

tg x = 1; x1 = pi/4 + pi*k

2) cos x = 1/2

x2 = +-pi/3 +

1)

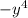
2)

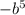
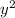
3)

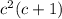
Пошаговое объяснение:

Правило: за скобки выносим множитель с меньшей степенью.

Когда выносим общий множитель, то каждый множитель делим на эоот общий множитель.

Пример 1:

1) В числителе выносим за скобки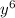 т.к. 6 меньше 8.

2) В скобках остается , потому что мы разделили все на

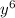
3) В знаменателе выносим за скобки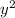 т.к. 2 меньше 4.

4) В скобках остается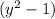 , потому что мы разделили все на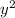

5) Вынесем знак минус за скобки в знаменателе. Когда выносим минус за скобки, то слагаемые в скобки меняют свои знаки на противоположные. Получаем: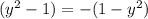 . Это было сделано для того, чтобы дробь можно было сократить.

6) Сокращаем скобку в числителе и знаменателе.

7) Сокращаем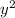 и  .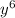

8) Записываем ответ. Не забываем про знак минус перед ним.

Пример 2:

Решается аналогично примеру 1 по такому же алгоритму.

Пример 3:

1) Вынесли общие множители за скобки в числителе и знаменателе (по правилу выше).

2) Скобка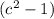 представляет собой формулу сокращенного умножения "разность квадратов" (я записала ее ниже).

3) Расписываем формулу в числителе.

4) Сокращаем скобку в числителе и знаменателе.

5) Сокращаем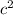 и .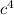

6) Записываем ответ.