Из вершины С проведем прямую параллельную диагонали BD до пересечения на продолжении прямой AD. Четырехугольник BCFD является параллелограммом, DF = BC, тогда по свойству средней линии трапеции
Поскольку диагонали перпендикулярны друг другу, то ∠ACF = 90°, тогда по теореме Пифагора найдем AF
Следовательно, - средняя линия трапеции.
Площадь прямоугольного треугольника ACF равна , с другой стороны она равна , приравнивая площади, мы получим
ответ: средняя линия трапеции равна 25/2, а высота - 12.
Из вершины С проведем прямую параллельную диагонали BD до пересечения на продолжении прямой AD. Четырехугольник BCFD является параллелограммом, DF = BC, тогда по свойству средней линии трапеции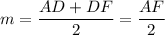
Поскольку диагонали перпендикулярны друг другу, то ∠ACF = 90°, тогда по теореме Пифагора найдем AF
Следовательно,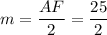 - средняя линия трапеции.
- средняя линия трапеции.
Площадь прямоугольного треугольника ACF равна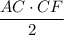 , с другой стороны она равна
, с другой стороны она равна 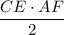 , приравнивая площади, мы получим
, приравнивая площади, мы получим
ответ: средняя линия трапеции равна 25/2, а высота - 12.