Для всіх додатніх a b c d доведіть що

Воспользуемся неравенством Коши для среднего арифметического и среднего геометрического n неотрицательных чисел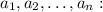

которое можно переписать в виде

В нашем случае получаем

Скористаємось нерівністю Коші

a/b + b/c ≥ 2√(a/b·b/c); a/b + b/c ≥ 2√(a/c);

c/d + d/a ≥ 2√(c/d·d/a); c/d + d/a ≥ 2√(c/a);

a/b + b/c + c/d + d/a ≥ 2√(a/c) + 2√(c/a) ≥ 2√(2√(a/c) · 2√(c/a))

a/b + b/c + c/d + d/a ≥ 4√(√((a/c) · (c/a)));

a/b + b/c + c/d + d/a ≥ 4√(√1);

a/b + b/c + c/d + d/a ≥ 4