Доказать что (6^2n-1 +1) делится на 7 - вопрос №621171714402 от Artem6776 24.01.2022 05:25

Question

Математика: Доказать что (6^2n-1 +1) делится на 7

Artem6776 · Answer

Применим здесь метод математической индукции.
1) При n=1 имеем:
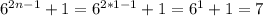
$6^{2n-1}+1= 6^{2*1-1}+1= 6^{1}+1 = 7$
7 делится на 7
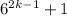2) Предположим, что для некоторого k число $6^{2k-1}+1$ кратно 7
Докажем, что это число будет кратно 7 для k+1:
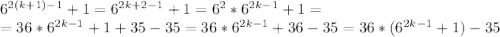
$6^{2(k+1)-1}+1= 6^{2k+2-1}+1=6^{2}*6^{2k-1}+1=\\ =36*6^{2k-1}+1+35-35=36*6^{2k-1}+36-35=36*(6^{2k-1}+1)-35$
Выражение в скобках делится на 7 согласно нашему предположению, и умноженное на 36, оно всё равно делится на 7 :)
Число -35 также делится на 7.
Значит и их сумма тоже делится на 7, что и требовалось доказать...