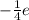1) 3 1/18 - 1/9 = 3×18+1 / 18 - 1/9 = 55/18 - 1/9 (мы перевели 3 1/18 в неправильную дробь)=55×9 / 18×9 − 1×18 / 9×18 = 495 / 162 − 18 / 162 (привели к общему знаменателю) = 495 − 18 / 162 = 477 / 162 = 53×9 / 18×9 = 53 / 18 ( Нахождение НОД и сокращение дроби) =17+2×18 / 18(Выделение целой части) = 2 17/182) 3 17/27 - 2 13/18 = (Перевод смешаных дробей в обыкновенные) 3×27 + 17 /27 − 2×18 + 13 / 18 = 98 /27 − 49 /18= (Приведение к общему знаменателю) 98×18 /27×18 − 49×27 /18×27 = 1764 /486 − 1323 /486= (Вычитание) 1764 − 1323 /486 = 441 /486= 49×9 /54×9 = 49 /54Остальные по такому же принципуобъясняю как найти общий знаменатель например один знаменатель делится на другой знаменательнапример у нас есть вычитание 4/6 - 1/3 Мы домножаем дробь 1/3 на число, чтоб в знаменателе получилось 6 то есть 1/3 мы умнажаем на 2 (всю дробь) и у нас получается 2/6 ⇒ 4/6 -2/6 = 2/6 = 1/3если у чисел нет общего нок, то мы умножаем числа друг на друга
например 4/8-3/9= 4*9/8*9 - 3*8/9*8 = 36/72 - 24/72= 12/72 сокращаем и получаем 1/6
Найдём производную функции y. y' = ((x+8)(x+9)e)'=((x+8)(x+9))'e=((x+8)'(x+9)+(x+8)(x+9)')e=((1+0)(x+9)+(x+8)(1+0))e=(2x+17)e
Приравняем производную к нулю, чтобы найти точки возможного экстремума. (2x+17)e=0 ⇔ 2x+17=0⇔ x = =-8.5. Найдем знаки производной слева и справа от точки -8.5 на промежутке [-10; -8], слева производная будет отрицательна, слева положительна, а значит функция y будет принимать в точке -8.5 наименьшее значение.
ответ: / - будем считать это дробью
1)2 17/18 2)49/54 3) 3 59/72 4)2 58 /63 5) 1 29 /36 6)3 50 /63
Пошаговое объяснение:
1) 3 1/18 - 1/9 = 3×18+1 / 18 - 1/9 = 55/18 - 1/9 (мы перевели 3 1/18 в неправильную дробь)=55×9 / 18×9 − 1×18 / 9×18 = 495 / 162 − 18 / 162 (привели к общему знаменателю) = 495 − 18 / 162 = 477 / 162 = 53×9 / 18×9 = 53 / 18 ( Нахождение НОД и сокращение дроби) =17+2×18 / 18(Выделение целой части) = 2 17/182) 3 17/27 - 2 13/18 = (Перевод смешаных дробей в обыкновенные) 3×27 + 17 /27 − 2×18 + 13 / 18 = 98 /27 − 49 /18= (Приведение к общему знаменателю) 98×18 /27×18 − 49×27 /18×27 = 1764 /486 − 1323 /486= (Вычитание) 1764 − 1323 /486 = 441 /486= 49×9 /54×9 = 49 /54Остальные по такому же принципуобъясняю как найти общий знаменатель например один знаменатель делится на другой знаменательнапример у нас есть вычитание 4/6 - 1/3 Мы домножаем дробь 1/3 на число, чтоб в знаменателе получилось 6 то есть 1/3 мы умнажаем на 2 (всю дробь) и у нас получается 2/6 ⇒ 4/6 -2/6 = 2/6 = 1/3если у чисел нет общего нок, то мы умножаем числа друг на друганапример 4/8-3/9= 4*9/8*9 - 3*8/9*8 = 36/72 - 24/72= 12/72 сокращаем и получаем 1/6
Пошаговое объяснение:
Найдём производную функции y. y' = ((x+8)(x+9)e)'=((x+8)(x+9))'e=((x+8)'(x+9)+(x+8)(x+9)')e=((1+0)(x+9)+(x+8)(1+0))e=(2x+17)e
Приравняем производную к нулю, чтобы найти точки возможного экстремума. (2x+17)e=0 ⇔ 2x+17=0⇔ x = =-8.5. Найдем знаки производной слева и справа от точки -8.5 на промежутке [-10; -8], слева производная будет отрицательна, слева положительна, а значит функция y будет принимать в точке -8.5 наименьшее значение.
=-8.5. Найдем знаки производной слева и справа от точки -8.5 на промежутке [-10; -8], слева производная будет отрицательна, слева положительна, а значит функция y будет принимать в точке -8.5 наименьшее значение.
Найдем y(-8.5)= (-8.5+8)e(-8.5+9)= -0.5*e*0.5=-0.25e=