Для выражение положительно. Сделаем преобразования, эквивалентные на данном множестве: .
Пусть строго монотонные непрерывные функции (и дифф. на рассматриваемом множестве). Тогда тоже монотонна на этом множестве. Достаточно показать, что не имеет корней: , где каждое из множителей не обращается в нуль на рассматриваемом множестве. (Поправьте, если неправ).
Рассмотрим функцию . Докажем, что она монотонна при положительных : .
Используя вышеизложенные рассуждения, приходим к выводу: монотонна при положительных значениях . (Можно и проще: просто поделить на числитель и знаменатель).
Для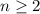 выражение
выражение 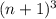 положительно. Сделаем преобразования, эквивалентные на данном множестве:
положительно. Сделаем преобразования, эквивалентные на данном множестве: 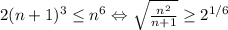 .
.
Пусть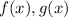 строго монотонные непрерывные функции (и дифф. на рассматриваемом множестве). Тогда
строго монотонные непрерывные функции (и дифф. на рассматриваемом множестве). Тогда 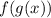 тоже монотонна на этом множестве. Достаточно показать, что
тоже монотонна на этом множестве. Достаточно показать, что ![[f(g(x))]'](/tpl/images/1358/5801/eb713.png) не имеет корней:
не имеет корней: ![[f(g(x))]'=f'(g(x))g'(x)](/tpl/images/1358/5801/a611e.png) , где каждое из множителей не обращается в нуль на рассматриваемом множестве. (Поправьте, если неправ).
, где каждое из множителей не обращается в нуль на рассматриваемом множестве. (Поправьте, если неправ).
Рассмотрим функцию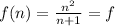 . Докажем, что она монотонна при положительных
. Докажем, что она монотонна при положительных 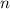 :
: 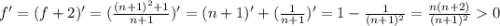 .
.
Используя вышеизложенные рассуждения, приходим к выводу: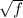 монотонна при положительных значениях
монотонна при положительных значениях 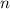 . (Можно и проще: просто поделить на
. (Можно и проще: просто поделить на 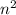 числитель и знаменатель).
числитель и знаменатель).
Для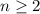 имеем:
имеем: 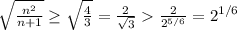 .
.