Решать следует от противного Предположим, что каждый ученик совершил неодинаковое количество ошибок То есть мы должны получить 30 разных неотрицательных чисел. Причем наибольшее из них - 14 Но неотрицательных чисел, меньше 14 всего 14, считая "0". Что значительно меньше общего числа учеников Потому наше утверждение не может быть верным, а значит кто-то из учеников обязательно допустил одинаковое количество ошибок Кроме Пети 29 учеников осталось, а вариантов сколько у них будет ошибок всего 14 . Значит 29\14=2 человека на вариант количества ошибок и 1 в остатке, так как остается 1, то по крайне мере 3 ученика сделали одинаковое количество ошибок.
2) 120 уч.
3) 90 очков
4) 40 уч.
Пошаговое объяснение:
Первая задача.Кр.запись.
250 руб - было всего
120 руб - потратила
? - часть своих денег Маша заплатила за мороженое
Решение.
120 / 250 =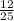
- Маша заплатила за мороженое
Вторая задача.Кр. запись.
420 уч. - всего
? уч. - ходят в муз. школу, но сказано, что ходят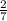
от всего кол-ва
Решение.
420 *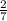
= 420 : 7 * 2 = 120 уч. - ходят в муз. школу
Третья задача.Кр. запись.
24 очка - получил капитан
? очков - получила команда, но сказано, что капитан получил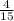
всех полученных очков.
Решение.
24 :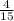
= 24 * 
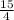= 24 : 4 * 15 = 90 очков - получила команда
Четвёртая задача.Кр.запись
в 3 классах поровну учащихся
? уч. - в каждом классе, но сказано, что если в каждый класс добавить по 3 уч., то всего в них будет 129 уч
Решение.
3 * 3 = 9 уч. - добавили
129 - 9 = 120 уч. - в 3 классах
120 : 3 = 40 уч. - в каждом классе.
Предположим, что каждый ученик совершил неодинаковое количество ошибок
То есть мы должны получить 30 разных неотрицательных чисел. Причем наибольшее из них - 14
Но неотрицательных чисел, меньше 14 всего 14, считая "0". Что значительно меньше общего числа учеников
Потому наше утверждение не может быть верным, а значит кто-то из учеников обязательно допустил одинаковое количество ошибок
Кроме Пети 29 учеников осталось, а вариантов сколько у них будет ошибок всего 14 . Значит 29\14=2 человека на вариант количества ошибок и 1 в остатке, так как остается 1, то по крайне мере 3 ученика сделали одинаковое количество ошибок.