Незнайка принимал таблетки каждый день и их количество равно номеру дня в месяце. Получаем арифметическую прогрессию, где первый член а₁= 1, разница d=1 , а сумма 465 . Формула суммы n членов арифметической прогрессии :
Подставим наши значения 6
D= 1²-4*(-930)= 1+3720=3721
x₁=
x₂=
корень х₂ не подходит, т.к. отрицательный , соответственно
количество дней , которые Незнайка принимал таблетки равно 30 дней .
Значит месяц, в котором принимал таблетки Незнайка, - апрель . Только в этом месяце 30 дней
В семье 5 детей
Старший 11 ³/₄ лет.
Переведем в более понятные единицы: 11 лет и (12*³/₄)= 9 месяцев
Каждый следующий младше на 2 ⁷/₁₂ или 2 года и (12*⁷/₁₂) =7 месяцев
теперь найдем возраст каждого ребенка
1 ребенок: 11 лет и 9 месяцев
2 ребенок: 11 г 9 м - 2 г 7м=9г 2м
3 ребенок: 9г 2м - 2г 7м= 8г 14м-2г 7м=6г 7м
4 ребенок: 6г 7м -2г 7м = 4 г
5 ребенок: 4г 0м - 2г 7м =3г 12м- 2г 7м=1г 5м
Если закономерность сохранится то разница должна быть 2г 7 м
Сейчас 5 ребенку 1г 5м , значит должно пройти еще 2г 7м -1г 5м= 1г 2м
Пошаговое объяснение:
Незнайка принимал таблетки каждый день и их количество равно номеру дня в месяце. Получаем арифметическую прогрессию, где первый член а₁= 1, разница d=1 , а сумма 465 . Формула суммы n членов арифметической прогрессии :
Подставим наши значения 6
D= 1²-4*(-930)= 1+3720=3721
x₁=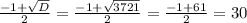
x₂=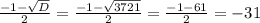
корень х₂ не подходит, т.к. отрицательный , соответственно
количество дней , которые Незнайка принимал таблетки равно 30 дней .
Значит месяц, в котором принимал таблетки Незнайка, - апрель . Только в этом месяце 30 дней