По условиям задачи, ни боцман, ни кок до разговора не знали, где закопан клад. Значит столбцами 5 и 6 можно пренебречь, так как в них есть однозначный ответ у кока, что противоречит условиям задачи. После разговора и коку и боцману стало известно, где клад. Значит надо искать такую пару значений, в которой одно из них после разговора утрачивает актуальность. Из пар a2 a3, b4 b5, c1 c3 такой является только вторая, поскольку 5 и 6 столбец не принимаются во внимание по причине, изложенной выше. Строкой d можно пренебречь, так как после разговора боцмана и кока в ней остаётся все так же 3 переменных.
1. Как известно, не бывает шестизначных номеров, начинающихся с нуля, поэтому надо подсчитать их количество и вычесть его из общего числа комбинаций. Число номеров, первая цифра у которых 0, найдем по формуле размещений с повторениями, «зафиксировав» ноль т.е. на каждом из пяти остальных возможных мест может встретиться любая из десяти цифр от
0 до 9.
Тогда число таких комбинаций:
= 100000
2. Первую букву можно выбрать , вторую при этом столькими же , тогда по правилу умножения можно составить буквенную часть номера.
Номера 0000 нет, всего можно составить 10*10*10*10-1=9999 числовых номеров.
90*9999=899910 разных номеров можно составить указанным
3. Количество вариантов выбора двух молодых людей из 10:
b4.
По условиям задачи, ни боцман, ни кок до разговора не знали, где закопан клад. Значит столбцами 5 и 6 можно пренебречь, так как в них есть однозначный ответ у кока, что противоречит условиям задачи. После разговора и коку и боцману стало известно, где клад. Значит надо искать такую пару значений, в которой одно из них после разговора утрачивает актуальность. Из пар a2 a3, b4 b5, c1 c3 такой является только вторая, поскольку 5 и 6 столбец не принимаются во внимание по причине, изложенной выше. Строкой d можно пренебречь, так как после разговора боцмана и кока в ней остаётся все так же 3 переменных.
вотак
Пошаговое объяснение:
1.
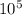= 100000
2. 899910
Пошаговое объяснение:
1. Как известно, не бывает шестизначных номеров, начинающихся с нуля, поэтому надо подсчитать их количество и вычесть его из общего числа комбинаций. Число номеров, первая цифра у которых 0, найдем по формуле размещений с повторениями, «зафиксировав» ноль т.е. на каждом из пяти остальных возможных мест может встретиться любая из десяти цифр от
0 до 9.
Тогда число таких комбинаций:
2. Первую букву можно выбрать , вторую при этом столькими же , тогда по правилу умножения можно составить буквенную часть номера.
Номера 0000 нет, всего можно составить 10*10*10*10-1=9999 числовых номеров.
90*9999=899910 разных номеров можно составить указанным
3. Количество вариантов выбора двух молодых людей из 10:
C(10,2) = 10! / ( 2! · (10 - 2!) = 9 · 10 / 2 = 45.
Количество вариантов выбора двух девушек из 13:
C(13,2) = 13! / ( 2! · (13 - 2!) = 12 · 13 / 2 = 78.
Общее число исходов при выборе однополых пар.
Сложим количество исходов для девушек и количество исходов для молодых людей.
N = C(10,2) + C(13,2) = 45 + 78 = 123.
ответ: Существует 123 исхода.