I вариант Упростите выражения.
m * 27 * 5 =
35 * k * 2 =
2. Упростите выражение 36х + 124 + 16x и найдите его значение при х = 5; х = 10.
3. Найдите значения выражений.
208 896 : 68 + (10 403 – 9896) * 204 =
(31-19)2 + 53 =
4. В двух зрительных залах кинотеатра 624 места. В одном зале в 3 раза больше мест, чем в другом. Сколько мест в меньшем зрительном зале?
5. Решите уравнения.
9у – 3у = 666
3х + 5х = 1632
6*. У Лены столько же монет по 2 руб., сколько и по 5 руб. Все монеты в сумме составляют 56 руб. Сколько монет по 2 руб. у Лены?

Показать ответ

Ответ:

AlinaMein14

20.10.2020 18:41

а) да; б) нет; в) 972

Пошаговое объяснение:

а) Пусть геометрическая прогрессия имеет знаменатель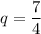 $q=\dfrac{7}{4}$ . Тогда получим последовательность 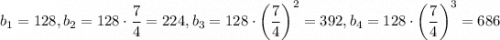$b_1=128,b_2=128\cdot\dfrac{7}{4}=224,b_3=128\cdot\left(\dfrac{7}{4}\right)^2=392,b_4=128\cdot\left(\dfrac{7}{4}\right)^3=686$ . Число 686 может быть записано на доске.

б) Заметим, что знаменатель прогрессии q не может быть иррациональным числом: в противном случае второй член прогрессии b₂ = 128q — иррациональное число, что противоречит условию. Значит, q — рациональное число.

Предположим, что 496 является n-ным членом последовательности. Тогда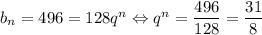 $b_n=496=128q^n\Leftrightarrow q^n=\dfrac{496}{128}=\dfrac{31}{8}$ . Поскольку 31 — простое число, оно не является степенью какого-либо другого числа. Значит, n = 1, 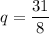$q=\dfrac{31}{8}$ . Тогда получаем геометрическую прогрессию 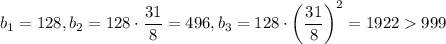$b_1=128,b_2=128\cdot\dfrac{31}{8}=496,b_3=128\cdot\left(\dfrac{31}{8}\right)^2=1922999$ — третий член последовательности не трёхзначный, что противоречит условию. Значит, прогрессии с членом 496 не существует.

в) Пусть A — наибольший возможный член геометрической прогрессии, по условию A < 1000. Тогда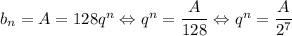 $b_n=A=128q^n\Leftrightarrow q^n=\dfrac{A}{128}\Leftrightarrow q^n=\dfrac{A}{2^7}$ . Число 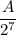$\dfrac{A}{2^7}$ является степенью некоторого рационального числа, значит, 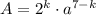$A=2^k\cdot a^{7-k}$ , где k — некоторое целое число из промежутка [0, 7], a — положительное нечётное число. Число представимо в таком виде, поскольку на 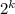2^k можно сократить, в знаменателе останется 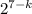$2^{7-k}$ , далее дробь несократима и является степенью n = 7 - k числа q: 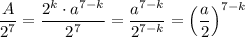$\dfrac{A}{2^7}=\dfrac{2^k\cdot a^{7-k}}{2^7}=\dfrac{a^{7-k}}{2^{7-k}}=\left(\dfrac{a}{2}\right)^{7-k}$ . 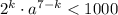Значит, $2^k\cdot a^{7-k}$ .

Переберём все k от 0 до 7:

k = 0:

. $2^7=128,3^7=2187\Rightarrow a\leq 2\Rightarrow a\leq 1\Rightarrow A\leq 1$ k = 1: 2a^6

. $2^6=64, 3^6=729\Rightarrow a\leq 2\Rightarrow a\leq 1\Rightarrow A\leq 2$ k = 2: 4a^5

. $3^5=243,4^5=1024\Rightarrow a\leq 3\Rightarrow A\leq 972$ k = 3: 8a^4

. $3^4=81,4^4=256\Rightarrow a\leq 3\Rightarrow A\leq 648$ k = 4: 16a^3

. $3^3=27, 4^3=64\Rightarrow a\leq 3\Rightarrow A\leq 432$ k = 5: 32a^2

. $5^2=25,6^2=36\Rightarrow a\leq 5\Rightarrow A\leq 800$ k = 6: 64a

k = 7:

— верно, A = 128.

Наибольшее значение A = 972. Покажем, что оно достигается. Пусть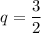 $q=\dfrac{3}{2}$ . Тогда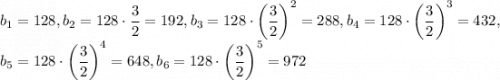 $b_1=128,b_2=128\cdot\dfrac{3}{2}=192,b_3=128\cdot\left(\dfrac{3}{2}\right)^2=288,b_4=128\cdot\left(\dfrac{3}{2}\right)^3=432,\\b_5=128\cdot\left(\dfrac{3}{2}\right)^4=648,b_6=128\cdot\left(\dfrac{3}{2}\right)^5=972$

Таким образом, наибольшее число, которое могла выписать Даша — 972.

0,0(0 оценок)

Ответ:

Dianaaaaaaaaaa03

08.03.2022 16:11

Надо налить молоко в 5-литровый кувшин, из 5 перелить в 7-лит Затем ещё раз налить в 5-лит. и из него долить в 7-лит. 2 литра молока. На этом этапе мы имеем: в 12лит. - 2л. 5лит. - 3л. 7лит. -7л. Теперь из 7лит. -7л. переливаем в 12лит и получаем 9л. А из 5лит. - 3л. выливаем в 7лит. имеем: в 12лит. 9л. 5лит. -пусто 7лит. -3л. Далее переливаем из 12лит. в 5лит. -5л. , а из 5лит. в 7лит. может поместится только 4 литра молока т. к. в 7лит. уже есть3л. , следовательно в 5лит. кувшине остался 1 литр

0,0(0 оценок)

Популярные вопросы: Математика