В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Пошаговое объяснение:
Точка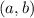
на комплексной плоскости изображает число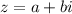 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа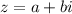
будет являться число 
.
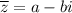В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси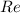
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
120 = 2³ · 3 · 5
300 = 2² · 3 · 5²
100 = 2² · 5²
наименьшее общее кратное = 2³ · 3 · 5² = 600
480 = 2^5 · 3 · 5
216 = 2³ · 3³
144 = 2^4 · 3²
наименьшее общее кратное = 2^5 · 3³ · 5 = 4320
105 = 3 · 5 · 7
350 = 2 · 5² · 7
140 = 2² · 5 · 7
наименьшее общее кратное = 3 · 5² · 7 · 2² = 2100
280 = 2³ · 5 · 7
140 = 2² · 5 · 7
224 = 2^5 · 7
наименьшее общее кратное = 2^5 · 5 · 7 = 1120
подробнее - на -