Итоговая контрольная работа в формате ОГЭ.
Инструкция к выполнению работы: все задания части 1 выполняем с подробным решением, 1 оценка будет выставлена по алгебре (первые семь заданий),2 оценка будет выставлена по геометрии (8-12 задания). Дополнительная часть 2 выполняется по желанию и на отдельную оценку. Сдать работу до 12.00
Часть 1.
1.Решите квадратное уравнение: 2х2 – 11х + 12 = 0.
2.Решите неравенство
3.Решите систему неравенств
4.У выражение: а) ;
б)
5.У выражение .
6.У выражение и найдите его значение при . В ответ запишите
полученное число.

7.На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу . Какая это точка?

8.Пожарную лестницу длиной 13 м приставили к окну пятого этажа дома. Нижний конец лестницы отстоит от стены на 5 м.
На какой высоте расположено окно? ответ дайте в метрах

9.Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы,
равные 30° и 45° соответственно.

10. AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. ответ дайте в градусах.

11.На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите рас стояние от точки А до прямой ВС. ответ выразите в сантиметрах.

12. Укажите номера верных утверждений.
1) Если три стороны одного треугольника равны трём сторонам другого треугольника, то такие треугольники равны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Если утверждений несколько, запишите их номера в порядке возрастания.

Часть 2

⦁ Решите уравнение: .
⦁ Теплоход проходит по течению реки до пункта назначения 176 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.

Показать ответ

Ответ:

Ludo4ka123

05.02.2020 12:07

Пошаговое объяснение:

Обычно на вопрос задачи дают неправильный ответ: 25 носков. Если бы в задаче спрашивалось, сколько носков следует взять из ящика, чтобы среди них было по крайней мере 2 носка различного цвета, то правильный ответ действительно был бы таким: 25 носков. Но в нашей задаче речь идет о том, чтобы среди взятых из ящика носков по крайней мере 2 носка были одного цвета, поэтому правильный ответ задачи иной: 3 носка. Если я возьму из ящика 3 носка, то они либо все будут одного цвета (и в этом случае я заведомо смогу выбрать из них по крайней мере 2 носка одного цвета), либо 2 носка будут одного цвета, а третий носок другого, что позволит мне также составить пару одноцветных носков.

0,0(0 оценок)

Ответ:

Heicioe

05.02.2020 12:07

5,4кг краски потребуется, чтобы покрасить все неокрашенные грани маленьких кубиков.

Пошаговое объяснение:

1000=10³

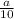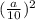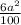Пусть а - сторона большого куба, тогда сторона маленького куба в 10 раз меньше, т.е. $\frac{a}{10}$ . У куба 6 одинаковых граней, имеющих форму квадрата. Площадь поверхности большого куба равна а²·6. Площадь поверхности маленького куба равна $(\frac{a}{10}) ^{2}$ ·6= $\frac{6a^{2} }{100}$ Площадь поверхности всех маленьких кубиков в тысячу раз больше 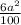$\frac{6a^{2} }{100}$ · 1000 = 60 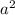$a^{2}$ . При этом окрашена была только поверхность большого куба, т.е. 6а². Значит, неокрашенными остались 60а²-6а²=54а². Для покраски одной грани большого куба понадобилось 100 грамм краски. Площадь одной грани большого куба равна а². Тогда, чтобы окрасить оставшиеся неокрашенными грани кубиков, краски потребуется в 54 раза больше, т.е. 54*100=5400гр=5,4кг