Заметим, что в сумме присутствуют числа 1, 11, а также числа с одним нулем, с двумя нулями, и так далее, с 50-ю нулями. Таким образом, в сумме всего записано 52 числа.
Удобно их сложить в столбик:
Отдельно сложим разряды единиц во всех числах и отдельно все остальные разряды.
Так как в разряде единиц во всех числах стоит 1, то сумма всех единиц равна 52.
Какие-либо разряды, кроме единиц, присутствуют в 51 числе. Поэтому, при суммировании всех остальных разрядов получим число, состоящее из 51 единицы.
Заметим, что в сумме присутствуют числа 1, 11, а также числа с одним нулем, с двумя нулями, и так далее, с 50-ю нулями. Таким образом, в сумме всего записано 52 числа.
Удобно их сложить в столбик:
Отдельно сложим разряды единиц во всех числах и отдельно все остальные разряды.
Так как в разряде единиц во всех числах стоит 1, то сумма всех единиц равна 52.
Какие-либо разряды, кроме единиц, присутствуют в 51 числе. Поэтому, при суммировании всех остальных разрядов получим число, состоящее из 51 единицы.
Сложим два получившихся числа:
Находим сумму цифр числа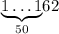 :
:
ответ: 58
48
Пошаговое объяснение:
Пусть геймдизайнер поставил порядковый номер дважды на платформу под номером k.
1+2+3+...+k+k+(k+1)+...+(n-1)=1323
1) 1+2+3+...+n>1323, n∈N
n(n+1)/2>1323
n²+n-2646>0
D=10585
Так как n>0, то
n>(-1+√10585)/2=50,9...>50
2) 1+2+3+...+(n-1)=1323-k<1323, n∈N
n(n-1)/2<1323
n²-n-2646<0
D=10585
Так как n>0, то
n<(1+√10585)/2=51,9...<52
3) 50<n<52, n∈N⇒n=51
1+2+3+...+k+k+(k+1)+...+50=1323
1+2+3+...+k+(k+1)+...+50=1323-k
1+2+3+...+50=1323-k
50·51/2=1323-k
1275=1323-k
k=1323-1275
k=48
Проверка
1+2+3+...+45+46+47+48+48+49+50=1323