Изображен острый угол. постройте отрезок сконцами на каждой стороне угла. покажите три разных варианта: так, чтобы полученный при этом тре- угольник был 1 прямоугольным, 2 тупоугольным, з остроугольным.
Нам нужно выразить число в виде степени с основанием . Для этого стоит вспомнить что при возведении степени в степень, основание (или число) степени остаётся без изменения, а показатели степеней перемножаются. То есть наглядно это выглядит так:
То есть нам нужно разложить 20 степень так, чтобы . К счастью это не составит проблем, так как 20 без проблем делится на 5, чтобы найти второе число, после которого наше число можно записать как число со степенью в степени. Поэтому если 20 поделить на 5, то мы получим 4. То есть исходя из формулы выше , а значит все число имеет вид:
n = 10
Пошаговое объяснение:
(n! + (n+2)!) / (n+1)! = 133/11
Заметим, что:
(n+1)! = n!*(n+1)
(n+2)! = n!*(n+1)(n+2)
Подставляем в уравнение.
(n! + n!*(n+1)(n+2)) / (n!*(n+1)) = 133/11
Сокращаем n!
(1 + (n+1)(n+2)) / (n+1) = 133/11
(1 + n^2 + 3n + 2) / (n+1) = 133/11
По правилу пропорции
11(n^2 + 3n + 3) = 133(n+1)
11n^2 + 33n + 33 = 133n + 133
11n^2 - 100n - 100 = 0
D = 100^2 - 4*11(-100) = 10000 + 4400 = 14400 = 120^2
n1 = (100 - 120)/22 = -20/22 < 0 - не подходит
n2 = (100 + 120)/22 = 220/22 = 10 - подходит.
Пошаговое объяснение:
Нам нужно выразить число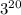
в виде степени с основанием 
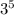. Для этого стоит вспомнить что при возведении степени в степень, основание (или число) степени остаётся без изменения, а показатели степеней перемножаются. То есть наглядно это выглядит так: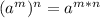 
То есть нам нужно разложить 20 степень так, чтобы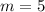
. К счастью это не составит проблем, так как 20 без проблем делится на 5, чтобы найти второе число, после которого наше число можно записать как число со степенью в степени. Поэтому если 20 поделить на 5, то мы получим 4. То есть исходя из формулы выше 
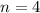, а значит все число имеет вид: