Р (выпала хотя бы одна единица) = 1 - Р (выпало ни 1 единицы) =
=
Р (выпало 2, 3, ... ,10 единиц) = 1 - Р (выпало 0 или 1 единица) =
Р (пересечение) = Р(выпало 2, 3, ... ,10 единиц) =
Р (выпало 2 или более единиц | выпала хотя бы одна единица) =
При решении мы пользовались формулой условной вероятности:
Р (выпала хотя бы одна единица) = 1 - Р (выпало ни 1 единицы) =
=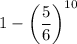
Р (выпало 2, 3, ... ,10 единиц) = 1 - Р (выпало 0 или 1 единица) =
=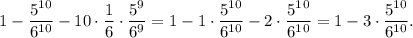
Р (пересечение) = Р(выпало 2, 3, ... ,10 единиц) =
=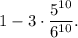
Р (выпало 2 или более единиц | выпала хотя бы одна единица) =
=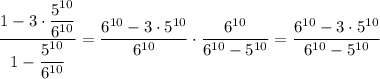
При решении мы пользовались формулой условной вероятности: