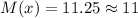Математическое ожидание - сумма попарных произведений значений случайной величины на вероятности, с которыми эти величины достигаются.
То есть, если значение достигается с вероятностью , значение - с вероятностью , и так далее, значение - с вероятностью , то математическое ожидание:
Математическое ожидание показывает среднее или наиболее вероятное значение случайной величины. В единичном испытании математическое ожидание равно вероятности события.
Для вычисления мат.ожидания как ожидаемого числа вопросов используем формулу:
, где - вероятность осуществления некоторого события, - число повторений.
В нашем случае, - вероятность того, что очередной вопрос не из группы "спринт", - число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
Поскольку вопросов не из группы "спринт" , а общее число вопросов , то вероятность того, что очередной вопрос не из группы "спринт" равна:
Число вопросов группы "спринт":
Тогда:
Конечно, можно действовать по первой формуле.
Для этого рассмотрим возможные количества вопросов не из группы "спринт", которые могли оказаться в группе "спринт". Это количества: 0, 1, 2, ..., 17, 18.
Найдем вероятности осуществления этих возможностей. Так как общий смысл сохраняется во всех ситуациях, то рассмотрим нахождение вероятности в общем виде - найдем с какой вероятностью i вопросов не из группы "спринт" попадут в группу "спринт".
Число выбрать вопросы в группу "спринт" с учетом этого условия соответствует тому, что из 18 вопросов не группы "спринт" мы выберем некоторые i штук, а остальные (30-i) штук мы выберем из 30 вопросов группы "спринт". Итоговое число благоприятных комбинаций: .
Общее число выбрать вопросы в группу "спринт" соответствует тому, что из всех 48 вопросов мы выберем некоторые 30 штук. Общее число комбинаций: .
Тогда, ситуации, что в группе "спринт" окажется i вопросов не из группы "спринт", соответствует вероятность .
Запишем математическое ожидание как сумму попарных произведений значений на вероятность:
Можно попробовать упростить эту формулу:
Далее нужно каким-либо досчитать эту величину. Вычисления дают полученный ранее результат:
Учитывая контекст вопроса, а именно, что мат.ожидание соответствует числу вопросов, попавших в группу "спринт", запишем также округленное до целого числа значение мат.ожидания:
Скубанью было связано творчество известного писателя, автора книг "нравы растеряевой улицы", "власть земли" и многих других, г.и. успенского (1842-1902 впервые побывавшего здесь проездом в 1882 г., направляясь в баку и тифлис. затем в 1885 г. - тоже проездом во владикавказ. в 1886 г. он совершил специальную поездку в кубанскую область и черноморский округ, двигаясь из ростова-на-дону в тихорецкую, екатеринодар, новороссийск, темрюк. в своих очерках "люди всякого звания" г.успенский писал, что, несмотря на то что поездка его "была поспешна и непродолжительна, разнообразие впечатлений, мест и всякого звания людей было настолько обильно", что он "не мог и пожелать ничего большего". "нигде, думается мне, - подчеркивал писатель, - не скопилось так много, как на кавказе, явлений жизни данной минуты, рисующих наши порядки, отношения и настроения, и нигде нет такого разнообразия местных условий, способствующих, чтобы разные порядки, вовсе одни на другие непохожие, уживались почти рядом друг с другом. то, что в россии надобно изучать по отдельным областям великороссии, малороссии, волыни или казанской татарщины, - все это можно видеть здесь как бы в образчиках, сгруппированных на незначительных пространствах места, точно в музее". резкие социальные контрасты отразил в своих произведениях м. горький , побывавший на кубани не один раз . в рассказах "мой спутник", "два босяка", "чужие люди", "дед архип и ленька", "женщина" и др. отражены непосредственные наблюдения автора над жизнью в кубанских станицах, в одной из которых он сам нанялся на работу к богатому казаку молотить хлеб и где стал свидетелем гибели товарища по работе, ставшего жертвой машинной уборки зерна. в новороссийске побывал писатель а.п. чехов (1860-1904 первую же свою поездку в наш край чехов совершает в июле 1888 г., путешествуя вдоль черного моря, начиная от новороссийска. впечатления от увиденного позднее нашли отражение в повести "дуэль". в последующем а.п. чехов неоднократно бывал на кубани(4 раза), встречаясь с "городом будущего" - новороссийском. в новороссийске с 1885 г. жил и работал секретарем местной таможни брат чехова, александр павлович (1855— 1913 тоже писатель. здесь он приобрел участок земли и построил свой дом. в редкие перерывы между служебными и хозяйственными делами он продолжает творить. к январю 1886 г. у него уже было заготовлено восемнадцать рассказов и по совету младшего брата новороссийский таможенник приступил к созданию книга. "пишу теперь ревностно и сознательно большую вещь, - сообщает он антону павловичу, - обдумываю каждую строку, и дело подвигается поэтому медленно. пишу я "город будущего" и копирую новороссийск, излагая свои наблюдения и впечатления, почерпнутые на " тесно были связаны жизнь и творчество с черноморским побережьем кубани писателя и публициста в.г. короленко (1853-1921 в джанхоте, недалеко от земельного участка и дома ф.а .щербины, он построил дачу для своего больного брата иллариона и начиная с 1900 г. почти ежегодно сам со своей семьей посещал это красивое место. здесь он написал очерк о жизни уральских казаков ("у казаков", 1901 рассказы «постройка дома» и «ушел! », переписал повесть «без языка» в 1964 г. по инициативе геленджикского -краеведческого музея в джанхоте был открыт мемориально- музей писателя. с в.г. короленко был дружен писатель-публицист с.и. васюков (1854-1908 который в 1903 г. приобрел на черноморском побережье кавказа (в архипо-осиповке) свое имение, в нескольких десятках километров от джанхота здесь он подготовил свои книги "край гордой красоты", "типы и характеры. кавказское черноморское побережье", на первую из которых дал отзыв в.г.короленко, отметивший, что "край гордой красоты" издан прекрасно и привлечет в черноморскую губернию туристов. жизнь писателя трагически оборвалась в 1908 г., он был убит бандитами, напавшими на него в архипо – осиповке, и похоронен на местном кладбище. в разное время около двадцати лет прожил на кубани и в черноморье писатель ф.в. гладков (1883-1958 свою творческую жизнь он начал сравнительно рано: ещё учась в екатеринодарском шестиклассном училище, писал свои рассказы и затем печатал их в "кубанских областных ведомостях" (1900-1902 самым известным его произведением является роман "цемент", написанный уже в годы гражданской войны. на кубани ф.в.гладков был редактором городской газеты «красное черноморье» и организатором местной системы народного образования в новороссийске. в 1921 года переселился в москву, где в 1923 году вошёл в пролетарское писательское объединение «кузница». образ кубани в второй половины xix века – это образ богатой и плодородной земли, бурно развивающейся окраины россии.здесь резкие контрасты между бедностью и богатством, всевластие хозяев и бесправие работниковздесь воля и зажиточность соседствуют с социальной несправедливостью
Математическое ожидание - сумма попарных произведений значений случайной величины на вероятности, с которыми эти величины достигаются.
То есть, если значение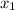 достигается с вероятностью
достигается с вероятностью 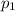 , значение
, значение  - с вероятностью
- с вероятностью  , и так далее, значение
, и так далее, значение 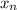 - с вероятностью
- с вероятностью 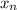 , то математическое ожидание:
, то математическое ожидание:
Математическое ожидание показывает среднее или наиболее вероятное значение случайной величины. В единичном испытании математическое ожидание равно вероятности события.
Для вычисления мат.ожидания как ожидаемого числа вопросов используем формулу:
В нашем случае, - вероятность того, что очередной вопрос не из группы "спринт",
- вероятность того, что очередной вопрос не из группы "спринт", 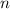 - число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
- число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
Поскольку вопросов не из группы "спринт"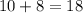 , а общее число вопросов
, а общее число вопросов  , то вероятность того, что очередной вопрос не из группы "спринт" равна:
, то вероятность того, что очередной вопрос не из группы "спринт" равна:
Число вопросов группы "спринт":
Тогда:
Конечно, можно действовать по первой формуле.
Для этого рассмотрим возможные количества вопросов не из группы "спринт", которые могли оказаться в группе "спринт". Это количества: 0, 1, 2, ..., 17, 18.
Найдем вероятности осуществления этих возможностей. Так как общий смысл сохраняется во всех ситуациях, то рассмотрим нахождение вероятности в общем виде - найдем с какой вероятностью i вопросов не из группы "спринт" попадут в группу "спринт".
Число выбрать вопросы в группу "спринт" с учетом этого условия соответствует тому, что из 18 вопросов не группы "спринт" мы выберем некоторые i штук, а остальные (30-i) штук мы выберем из 30 вопросов группы "спринт". Итоговое число благоприятных комбинаций: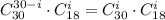 .
.
Общее число выбрать вопросы в группу "спринт" соответствует тому, что из всех 48 вопросов мы выберем некоторые 30 штук. Общее число комбинаций: .
.
Тогда, ситуации, что в группе "спринт" окажется i вопросов не из группы "спринт", соответствует вероятность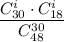 .
.
Запишем математическое ожидание как сумму попарных произведений значений на вероятность:
Можно попробовать упростить эту формулу:
Далее нужно каким-либо досчитать эту величину. Вычисления дают полученный ранее результат:
Учитывая контекст вопроса, а именно, что мат.ожидание соответствует числу вопросов, попавших в группу "спринт", запишем также округленное до целого числа значение мат.ожидания:
ответ: