Ка
хараад
iliml
.
составили 2720 КГ?
ВАРИАНТ № 2
1. Выполните действия: а)1,82 — 0,84: 0,7; б)(8 +62):11.
2. Решите уравнение: а) 14а-11a=41,22 ;b) бу+бу=132
3. На 1 см-поверхности расходуется 4 грамма краски. Сколько кг краски
потребуется для окрашивания куба с ребром 25 дм?
4. За 5 одинаковых книг и 3 ручки, стоимостью по 2000 сумов каждая, Жасур
заплатил 41000 сумов. Найдите цену книги.
5. 45% из 320 туристов составляют мужчины. Определите количество
женщин.
24·x²–34·x+25·y²=39
Пошаговое объяснение:
Пусть (x; y) координаты точки M, то есть M(x; y), d₁ – расстояние от точки M(x; y) до точки А(1; 0), а d₂ – расстояние от точки M(x; y) до прямой x=8.
Проекцией точки M(x; y) на ось Ох будет точкой В(x; 0) (см. рис). Тогда расстояние d₁ можем найти из прямоугольника треугольника AMB с катетами
АВ = (х–1) и ВM = у.
Применим теорему Пифагора: d₁²=(х–1)²+у².
Далее, расстояние от точки M(x; y) до прямой x=8 равно
d₂=|8–х|.
По условию задачи
5·d₁ = d₂ или 25·d₁² = d₂².
Получим уравнение:
25·((х–1)²+у²) = (8–х)².
Упростим уравнение:
25·x²–50·x+25+25·y²–x²+16·x=64
24·x²–34·x+25·y²=39.
Данная функция является квадратичной, и ее график — это парабола.
Сперва нужно определить коэффициенты а, b и c в формуле функции.
Формула абсциссы вершины параболы:
По графику видим, что абсцисса вершины равна 4.
Значит,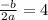 .
.
Выберем две точки с целочисленными координатами, принадлежащие параболе.
Возьмем вершину, т. А (4; 1) и т. В (2; -3).
Подставим координаты точек в формулу функции: абсциссу вместо х, а ординату вместо у.
Получаем два уравнения:
1)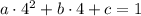
2)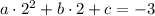
Составим систему уравнений:
Из первого уравнения выразим коэффициент b.
Сперва умножим обе части уравнения на знаменатель дроби:
Теперь умножим обе части на -1:
Из второго уравнения вычтем третье, чтобы избавиться от коэффициента c. Отдельно вычитаем левые, отдельно правые части:
Раскроем скобки:
Приведем подобные слагаемые:
Разделим обе части уравнения на 2 для удобства:
Подставим значение коэффициента b:
Теперь найдем коэффициент b, подставив найденное значение коэффициента а в уравнение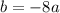 :
:
Подставим значения коэффициентов а и b в третье уравнение системы, чтобы найти коэффициент с:
Подставим найденные коэффициенты в формулу функции:
у = -х² + 8х - 15
Чтобы найти у(-19), подставим число -19 вместо аргумента:
ответ: -528.