1. Обратить внимание на аргументы. Здесь есть и х, и 2х.
Значит надо все аргументы свести к одному аргументу х,
применив формулу косинуса двойного аргумента
Уравнение :
Разложим на множители:
Произведение двух множителей равно 0 когда хотя бы один из них равен 0:
или
- однородное тригонометрическое уравнение первого порядка, делим на cosx ≠0
Так как
Применяем формулу
sinα - sinβ=
так как
так как синус - нечетная функция, то
Общий вид решения уравнения:
Это удобнее записать в виде серии двух ответов:
k=2m или k = 2n-1
О т в е т. ; ;
√3сosx-√2cos²x+√2sin²x+√3sinx=0
√3sinx+√3сosx-√2(cosx-sinx)(cosx+sinx)=0
(cosx+sinx)(√3-√2cosx+√2sinx)=0
cosx+sinx=0;tgx=-1; х=-π/4+πn; n∈Z;
(sinx-cosx)=-√(3/2)
(sinx-sin(π/2-x)=-√(3/2)
2sin(x-π/4)*cosπ/4=-√(3/2);
√2sin(x-π/4)=-√(3/2);
sin(x-π/4)=-√(3/4);
(x-π/4)=(-1)ⁿ⁺¹arcsin√0.75+πк; к∈Z
x=π/4+(-1)ⁿ⁺¹arcsin√0.75+πк; к∈Z
1. Обратить внимание на аргументы. Здесь есть и х, и 2х.
Значит надо все аргументы свести к одному аргументу х,
применив формулу косинуса двойного аргумента
Уравнение :
Разложим на множители:
Произведение двух множителей равно 0 когда хотя бы один из них равен 0:
или
Так как
Применяем формулу
sinα - sinβ=
так как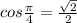
Общий вид решения уравнения:
Это удобнее записать в виде серии двух ответов:
k=2m или k = 2n-1
О т в е т.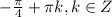 ;
; 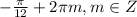 ;
; 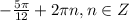
√3сosx-√2cos²x+√2sin²x+√3sinx=0
√3sinx+√3сosx-√2(cosx-sinx)(cosx+sinx)=0
(cosx+sinx)(√3-√2cosx+√2sinx)=0
cosx+sinx=0;tgx=-1; х=-π/4+πn; n∈Z;
(sinx-cosx)=-√(3/2)
(sinx-sin(π/2-x)=-√(3/2)
2sin(x-π/4)*cosπ/4=-√(3/2);
√2sin(x-π/4)=-√(3/2);
sin(x-π/4)=-√(3/4);
(x-π/4)=(-1)ⁿ⁺¹arcsin√0.75+πк; к∈Z
x=π/4+(-1)ⁿ⁺¹arcsin√0.75+πк; к∈Z