27 чисел
Пошаговое объяснение:
Пусть x, y — цифры двузначного числа (1 ≤ x ≤ 9, 0 ≤ y ≤ 9). Тогда
Первый множитель не меньше нуля, а второй не меньше -1.
Если y = 0, то произведение заведомо отрицательно, и все x подходят (+9 вариантов);
Если y = 1, то произведение равно нулю, все x подходят (+9 вариантов);
Если y = 2, то (+2 варианта);
Если y ≥ 3, то . При x ≥ 2 произведение больше единицы, поэтому для каждого y подходит ровно один x = 1 (+7 вариантов).
Итого 27 чисел.
27 чисел
Пошаговое объяснение:
Пусть x, y — цифры двузначного числа (1 ≤ x ≤ 9, 0 ≤ y ≤ 9). Тогда
Первый множитель не меньше нуля, а второй не меньше -1.
Если y = 0, то произведение заведомо отрицательно, и все x подходят (+9 вариантов);
Если y = 1, то произведение равно нулю, все x подходят (+9 вариантов);
Если y = 2, то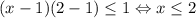 (+2 варианта);
(+2 варианта);
Если y ≥ 3, то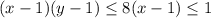 . При x ≥ 2 произведение больше единицы, поэтому для каждого y подходит ровно один x = 1 (+7 вариантов).
. При x ≥ 2 произведение больше единицы, поэтому для каждого y подходит ровно один x = 1 (+7 вариантов).
Итого 27 чисел.