, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).
Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен . Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:
Теперь высоту мы знаем и можем найти площадь трапеции:
2·(х+х+15°)=360°,2(2х+15°)=360°,2х+15°=360°:2, 2х+15°=180°,2х=180°-15°,2х=165°,х=165°:2, х=82,5°,
х+15°=82,5°+15°=97.5°
ответ: 82,5°,97.5°, 82,5°,97.5°
2. х-меньший угол ,(х+7.5°)-второй угол.Тогда
2· (х+(х+7.5°)=360°,2х+7,5°=180°,2х=180°-7.5°=172,5°
х=172°30':2=86°15'
х+7°30'=86°15'+7°30'=93°45'
ответ: 86°15'; 93°45'; 86°15'; 93°45'.
3. х-меньший угол,тогда 2х-больший угол,сумма углов 360°,поэтому
2(х+2х)=360°,6х=360°,х=360°:6=60°,тогда 2х=2·60°=120°
ответ: 60°,120°, 60°,120°.
ответ: 180.
Вот формула площади трапеции:
Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен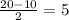
. Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:
Теперь высоту мы знаем и можем найти площадь трапеции:
Задача решена!