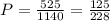При делении положительного числа на отрицательное в результате получается положительное число.
Рассмотрим эти два случая на примерах и убедимся в своём выборе:
1. При делении двух отрицательных чисел в результате получается положительное число.
Возьмём пример:
(-10) ÷ (-2) = 5 - получилось положительное число (так как при делении и умножении минус на минус даёт плюс), поэтому предложение верное.
2. При делении положительного числа на отрицательное в результате получается положительное число.
100 ÷ (-10) = -10 - получилось отрицательное число (так как минус на плюс даёт минус), поэтому предложение неверное.
а) 191/228
б) 1/114
в) 125/228
Пошаговое объяснение:
Число возможных элементарных исходов для выборки 3 из 20 приемников вычисляем по формуле:
С³₂₀ = = = 1140 (Это общее количество всех возможных комбинаций, когда из 20 приемников выбрали 3)
а) Число "нужных" комбинаций, когда выбрали 3 исправных приемника из 15 исправных:
С³₁₅=
Значит вероятность а) : (отношение нужных комбинаций ко всем возможным)
б) Число "нужных" комбинаций, когда выбрали 3 неисправных приемника из 5 неисправных:
С³₅=
Значит вероятность б) :
в) Число "нужных" комбинаций, когда выбрали 1 неисправный из 5 неисправных и 2 исправных приемника из 15 исправных равна произведению:
С¹₅ * С²₁₅ =
Значит вероятность в) :
При делении положительного числа на отрицательное в результате получается положительное число.
Рассмотрим эти два случая на примерах и убедимся в своём выборе:
1. При делении двух отрицательных чисел в результате получается положительное число.
Возьмём пример:
(-10) ÷ (-2) = 5 - получилось положительное число (так как при делении и умножении минус на минус даёт плюс), поэтому предложение верное.
2. При делении положительного числа на отрицательное в результате получается положительное число.
Возьмём пример:
100 ÷ (-10) = -10 - получилось отрицательное число (так как минус на плюс даёт минус), поэтому предложение неверное.
а) 191/228
б) 1/114
в) 125/228
Пошаговое объяснение:
Число возможных элементарных исходов для выборки 3 из 20 приемников вычисляем по формуле:
С³₂₀ =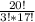
= 
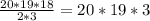= 1140 (Это общее количество всех возможных комбинаций, когда из 20 приемников выбрали 3)
а) Число "нужных" комбинаций, когда выбрали 3 исправных приемника из 15 исправных:
С³₁₅=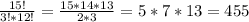
Значит вероятность а) :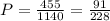
(отношение нужных комбинаций ко всем возможным)
б) Число "нужных" комбинаций, когда выбрали 3 неисправных приемника из 5 неисправных:
С³₅=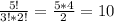
Значит вероятность б) :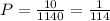
в) Число "нужных" комбинаций, когда выбрали 1 неисправный из 5 неисправных и 2 исправных приемника из 15 исправных равна произведению:
С¹₅ * С²₁₅ =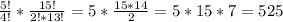
Значит вероятность в) :