ДИСКРЕНАЯ МАТЕТАТИКА 1.1. Множества заданий множеств. 1. Проиллюстрируйте с кругов Эйлера высказывание: «Все учащиеся 5 класса присутствовали на школьной спартакиаде». Решение: Выделим множества, о которых идет речь в высказывании: это множество учащихся некоторой школы (обозначим его за А), и множество учащихся 5 класса (обозначим его В). В данном высказывании утверждается, что все элементы множества В являются также и элементами множества А. По определению отношения включения это означает, что В А. Поэтому множество В надо изобразить внутри круга, изображающего множество А. 2. Задайте множество другим если это возможно): а) А = {х| xN, х ≤ 9}; б) А = {-4, -3, -2, -1, 0, 1, 2, 3, 4}; в) А = {х| xR, х 2 – 3 = 0}. Решение: а) Элементами множества А являются натуральные числа, которые меньше 9 и само число 9, значит, А = {1, 2, 3, 4, 5, 6, 7, 8, 9}; б) А = {х| xZ, |x| ≤ 4} – множество целых чисел, модуль которых не больше четырех; в) Элементами множества А являются корни уравнения х 2 – 3 = 0, значит, А = {- 3 , 3 }. 3. Изобразите на координатной прямой перечисленные множества: а) А = {х| xR, -1,5 ≤ х ≤ 6,7}; б) М = {х| xN, 4х - 14 < 0}; в) С = {х| xZ, -5 < х <2}; г) Н = {х| xZ, |x| < 7}. Решение: ответы показаны на рисунке: а) А = [-1,5; 6,7] б) М = {1, 2, 3} в) С = (-5; 2) г) Н = {-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6} 4. Задайте числовое множество описанием характеристического свойства элементов: а) (0; 11); б) [-12,3; 1,1); в) [-5; 3]; г) (- ∞; -102,354]. Решение: а) А = {х| xR, 0 < х <11}; б) С = {х| xR, -12,3 ≤ х < 1,1}; в) А = {х| xR, -5 ≤ х ≤ 3}; г) Р = {х| xR, х ≤ -102,354}. 5. Даны множества: а) К = {у| у = 1, если уN, то у + 1N}, У = {у| уZ, у > 0}; б) К = Ø, У = {Ø}; в) К = {с, п, р}, У = {{с, п}, р }. Равны ли множества К и У
2) 120 уч.
3) 90 очков
4) 40 уч.
Пошаговое объяснение:
Первая задача.Кр.запись.
250 руб - было всего
120 руб - потратила
? - часть своих денег Маша заплатила за мороженое
Решение.
120 / 250 =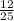 - Маша заплатила за мороженое
- Маша заплатила за мороженое
Вторая задача.Кр. запись.
420 уч. - всего
? уч. - ходят в муз. школу, но сказано, что ходят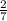 от всего кол-ва
от всего кол-ва
Решение.
420 *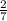 = 420 : 7 * 2 = 120 уч. - ходят в муз. школу
= 420 : 7 * 2 = 120 уч. - ходят в муз. школу
Третья задача.Кр. запись.
24 очка - получил капитан
? очков - получила команда, но сказано, что капитан получил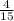 всех полученных очков.
всех полученных очков.
Решение.
24 :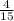 = 24 *
= 24 * 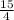 = 24 : 4 * 15 = 90 очков - получила команда
= 24 : 4 * 15 = 90 очков - получила команда
Четвёртая задача.Кр.запись
в 3 классах поровну учащихся
? уч. - в каждом классе, но сказано, что если в каждый класс добавить по 3 уч., то всего в них будет 129 уч
Решение.
3 * 3 = 9 уч. - добавили
129 - 9 = 120 уч. - в 3 классах
120 : 3 = 40 уч. - в каждом классе.