Для начала докажем неравенство методом математической индукции. При n = 1 неравенство имеет место. Далее, если оно имеет место при n, то для n+1 имеем
Последнее неравенство справедливо, так как
Существование и равенство нулю предела вытекает из неравенства
справедливого при всех .
Для начала докажем неравенство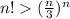 методом математической индукции. При n = 1 неравенство имеет место. Далее, если оно имеет место при n, то для n+1 имеем
методом математической индукции. При n = 1 неравенство имеет место. Далее, если оно имеет место при n, то для n+1 имеем
Последнее неравенство справедливо, так как
Существование и равенство нулю предела вытекает из неравенства