1. Определим какую часть заказа выполнит первый рабочий за один час 1 / 6 = 1/6 часть. 2. Определим какую часть заказа выполнит второй рабочий за один час 1 / 10 = 1/10 часть. 3. Теперь узнаем какую часть всего заказа смогут выполнить два рабочих, если они будут выполнять заказ одновременно. 1/6 + 1/10 = 5/30 + 3/30 = 8/30 заказа. 4. Узнаем какую часть заказа выполнят эти рабочие за 3 часа совместной деятельности. 8/30 * 3 = 24/30 заказа. 5. Далее определим какую часть заказа останется выполнить. 1 - 24/30 = 6/30 = 1/5 часть заказа. ответ: После трех часов совместной деятельности останется выполнить 1/5 часть всего заказа. . . . получается так)
Покажем, что никакие 2 числа из не могут давать одинаковые остатки от деления на n.
Пусть не так, и .
Но тогда их разность делится на n. Отсюда следует, с учетом взаимной простоты n и d, что делится на n. Но, нетрудно заметить, - противоречие.
Значит, числа дают различные остатки при делении на n. Но этих чисел ровно n - значит, среди них обязательно найдется число, дающее остаток 0 при делении на n. Противоречие с тем, что числа взаимно простые с n.
Это и означает, что числа n и d не взаимно простые.
2. Определим какую часть заказа выполнит второй рабочий за один час 1 / 10 = 1/10 часть.
3. Теперь узнаем какую часть всего заказа смогут выполнить два рабочих, если они будут выполнять заказ одновременно.
1/6 + 1/10 = 5/30 + 3/30 = 8/30 заказа.
4. Узнаем какую часть заказа выполнят эти рабочие за 3 часа совместной деятельности.
8/30 * 3 = 24/30 заказа.
5. Далее определим какую часть заказа останется выполнить.
1 - 24/30 = 6/30 = 1/5 часть заказа.
ответ: После трех часов совместной деятельности останется выполнить 1/5 часть всего заказа.
.
.
.
получается так)
Пусть не так, и и числа n и d взаимно простые.
Покажем, что никакие 2 числа из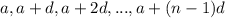 не могут давать одинаковые остатки от деления на n.
не могут давать одинаковые остатки от деления на n.
Пусть не так, и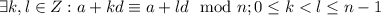 .
.
Но тогда их разность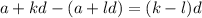 делится на n. Отсюда следует, с учетом взаимной простоты n и d, что
делится на n. Отсюда следует, с учетом взаимной простоты n и d, что 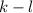 делится на n. Но, нетрудно заметить,
делится на n. Но, нетрудно заметить, 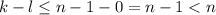 - противоречие.
- противоречие.
Значит, числа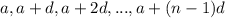 дают различные остатки при делении на n. Но этих чисел ровно n - значит, среди них обязательно найдется число, дающее остаток 0 при делении на n. Противоречие с тем, что числа
дают различные остатки при делении на n. Но этих чисел ровно n - значит, среди них обязательно найдется число, дающее остаток 0 при делении на n. Противоречие с тем, что числа 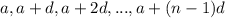 взаимно простые с n.
взаимно простые с n.
Это и означает, что числа n и d не взаимно простые.
Ч.т.д.