Слева видим функцию без параметра, а справа параметрическая прямая, вращающаяся вокруг точки . В таких случаях удобно строить отдельно левую (фиксированную) часть уравнения и правую (параметрическую) в координатах .
Для наглядности можно записать так:
Понятно, что в первой строке системы у нас график полуокружности, достигающий при или .
После его построения будем вращать прямую вокруг точки и искать удовлетворяющие условию расположения.
(см. прикрепленный файл)
В первом случае прямая касается полуокружности в ее верхней точке, так как наибольшее значение будет . В этом случае .
(см. объяснение)
Пошаговое объяснение:
Слева видим функцию без параметра, а справа параметрическая прямая, вращающаяся вокруг точки
. В таких случаях удобно строить отдельно левую (фиксированную) часть уравнения и правую (параметрическую) в координатах 
.
Для наглядности можно записать так:
Понятно, что в первой строке системы у нас график полуокружности, достигающий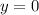
при 
или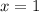 
.
После его построения будем вращать прямую вокруг точки
и искать удовлетворяющие условию расположения.
(см. прикрепленный файл)
В первом случае прямая касается полуокружности в ее верхней точке, так как наибольшее значение будет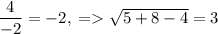
. В этом случае 
.
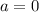Во втором случае прямая проходит через точк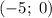и
и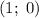 
.
Найдем соответствующие значения параметра:
Теперь осталось только сформировать ответ:
При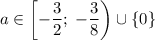
исходное уравнение имеет ровно один корень.
Задание выполнено!
Пошаговое объяснение:
изучать - одинаково, потому что это две взамно-обратные операции.
как умножение и деление (утрирую)
геометрический смысл обеих операций понятен
производная - тангенс наклона касательной к данной функции к оси икс
первообразная - площадь криволинейной трапеции под графиком функции построенной на оси икс
а вот реально вычислять производную проще чем искать первообразную, особенно если функция не табличная.
ведь практически для любой непрерывной функции можно найти производную, а вот первообразную можно найти далеко не для любой функции