На десяти одинаковых карточках написаны различные числа от 0 до 9 . определить вероятность того , что случайно составленное с данных карточек двузначное число делится на 18. (ответ 0,056) с решение + по какой формула.

1) Если учитывать все возможные числа от 01 до 99, то вероятность p ≈ 0,056

2) Если учитывать все возможные числа от 10 до 99, то вероятность p ≈ 0,062

Пошаговое объяснение:

Вероятность равна отношению благоприятных исходов (m) к общему количеству попыток (n).

Из множества чисел от 0 до 99 делятся на 18 следующие:

18; 36; 54; 72; 90.

Итого благоприятных исходов m = 5.

Найдем общее количество двузначных чисел, удовлетворяющих условию задачи.

Так как карточек с числами всего 10, по одной цифре от 0 до 9, то мы не можем составить числа вида 11; 22; ...; 99. Т.е. 9 чисел из числа двузначных нужно исключить.

1) Если к двузначным числам отнести составленные из двух карточек числа вида 01; 02 и т.д. (т.е. числа с незначащим нулем впереди), то всех двузначных чисел будет n = 99 - 9 = 90.

Тогда вероятность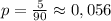

2) Если к двузначным числам мы не относим числа вида 01; 02; ...; 09, то всех двузначных чисел будет n = 99 - 9 - 9 = 81.

Тогда вероятность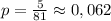   .