Всего трое ребят довольствовались 3+2 = 5 пакетиками фисташек, то бишь каждый съел по пакетика. Из трех пакетиков, купленных Вовой, он сам угостился этими самыми пакетика, а оставшимися поделился с Мишей. Из двух пакетиков, купленных Димой, он сам съел тоже пакетика, а остальную отдал Мише. Получается, что "вклады" щедрых ребят в лакомства Миши находятся в отношении 4:1. В таком же отношении они разделят плату. Пускай x — коэффициент пропорциональности. Тогда Вове причитается 4x рублей, а Диме — x рублей. По условию 4x+x = 2525, тогда 5x = 2525, x = 505.
Итак, Дима положит в карман 505 рублей, а Вова — 505×4 = 2020 рублей.
Вова получает 2020 рублей, Дима — 505 рублей
Пошаговое объяснение:
Всего трое ребят довольствовались 3+2 = 5 пакетиками фисташек, то бишь каждый съел по
пакетика. Из трех пакетиков, купленных Вовой, он сам угостился этими самыми 
пакетика, а оставшимися 
поделился с Мишей. Из двух пакетиков, купленных Димой, он сам съел тоже 
пакетика, а остальную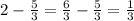 
отдал Мише. Получается, что "вклады" щедрых ребят в лакомства Миши находятся в отношении 4:1. В таком же отношении они разделят плату. Пускай x — коэффициент пропорциональности. Тогда Вове причитается 4x рублей, а Диме — x рублей. По условию 4x+x = 2525, тогда 5x = 2525, x = 505.
Итак, Дима положит в карман 505 рублей, а Вова — 505×4 = 2020 рублей.
190 (с учетом порядка)
37 (без учета порядка)
Пошаговое объяснение:
Нужно разложить 42 конфеты на 3 четные кучки.
Пусть есть некое разложение числа 42 в сумму трех четных натуральных слагаемых:
2n + 2m + 2r = 42
n + m + r = 21
n,m,r - произвольные натуральные числа.
Как видим, задача эквивалента нахождению разложений числа 21 в сумму трех произвольных натуральных чисел.
Рассмотрим сначала самый простой вариант. (важен порядок разбиения кучек)
То есть, например, 10,10,1 и 1,10,10 - это разные варианты.
Пусть на первом месте стоит число 1<=n<=19, тогда сумма остальных двух чисел равна: 21 - n
Число вариантов разбить 21 - n в виде суммы двух чисел с учетом порядка равна: 21 - n - 1 = 20 - n.
Тогда, число вариантов разбить 21 в сумма трех слагаемых с учетом порядка:
N = (20 -1) + (20 - 2) +(20 - 3) ... + (20 - 19) = 19 + 18 + 17 + 16 + 15... + 1 =
= 19*20/2 = 190 - сумма арифметической прогрессии.
Рассмотрим теперь уже более сложный вариант ( без учета порядка)
Число разложений в сумму трех одинаковых чисел равно 1 и равно:
7+7+7 = 21.
Найдем теперь число разложений в сумму трех чисел среди которых два числа равны (без учета порядка)
То есть такие варианты, где n = r
2n + m = 21
Откуда:
2<=2n<=20
1<=n<=10
То есть всего 9 вариантов, без учета варианта 7,7,7
Число вариантов разместить 2 одинаковых объекта и третий в определенном порядке равно трем.
Тогда число таких вариантов с учетом порядка равно: 3*9 = 27
Таким образом, пользуясь предыдущим результатом, можно найти число вариантов разложения в сумму трех различных натуральных чисел с учетом порядка:
190 - 27 - 1 = 190 - 28 = 162
Число вариантов переставить 3 различных объекта равно 3! = 6, тогда число таких вариантов без учета порядка: 162/6 = 27.
То есть общее число вариантов (без учета) порядка:
27 + 9 + 1 = 37