На доске написано 120 чисел. Среди их всевозможных попарных произведений ровно 2000 отрицательных. Какое наибольшее количество нулей могло быть среди чисел, написанных на доске.
Пусть было записано x положительных, y отрицательных и z нулей. Тогда x + y + z = 120, xy = 2000. Выразим из второго равенства y и подставим в первое: . Так как z должно быть наибольшим, значение выражения должно быть наименьшим. Так как x > 0, по неравенству о средних
Наименьшее значение достигается, когда оба слагаемых равны:
Вспомним, что x, z и 120 — целые числа, значит, 2000 / x — тоже целое число, то есть x — делитель числа 2000. Перебирая последовательно вверх числа от 45, приходим к x = 50. . Перебирая последовательно вниз числа от 44, приходим к x = 40. . Наибольшее количество нулей — 30.
30
Пошаговое объяснение:
Пусть было записано x положительных, y отрицательных и z нулей. Тогда x + y + z = 120, xy = 2000. Выразим из второго равенства y и подставим в первое: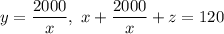
. Так как z должно быть наибольшим, значение выражения 
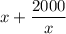должно быть наименьшим. Так как x > 0, по неравенству о средних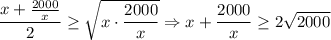 
Наименьшее значение достигается, когда оба слагаемых равны:
Вспомним, что x, z и 120 — целые числа, значит, 2000 / x — тоже целое число, то есть x — делитель числа 2000. Перебирая последовательно вверх числа от 45, приходим к x = 50.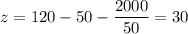
. Перебирая последовательно вниз числа от 44, приходим к x = 40. 
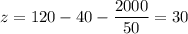. Наибольшее количество нулей — 30.