Так как диагональ ромба принадлежит оси абсцисс, и из того, что диагонали ромба перпендикулярны, узнаём, что вторая диагональ ромба принадлежит оси ординат.
Так как диагонали ромба при пересечении делятся пополам, а середина диагонали — начало координат, определяем положение вершины — она симметрична точке относительно . Значит .
Площадь ромба равна 4 (см. рисунок)
Пошаговое объяснение:
Так как диагональ ромба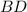 принадлежит оси абсцисс, и из того, что диагонали ромба перпендикулярны, узнаём, что вторая диагональ ромба
принадлежит оси абсцисс, и из того, что диагонали ромба перпендикулярны, узнаём, что вторая диагональ ромба 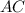 принадлежит оси ординат.
принадлежит оси ординат.
Так как диагонали ромба при пересечении делятся пополам, а середина диагонали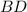 — начало координат, определяем положение вершины
— начало координат, определяем положение вершины 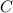 — она симметрична точке
— она симметрична точке 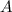 относительно
относительно 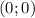 . Значит
. Значит 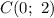 .
.
Ромб изображен на рисунке.
Вычислим площадь ромба по формуле
поэтому