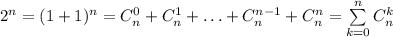Пошаговое объяснение:
Количество построить k-угольник по 101 точке - .
Тогда количество построить все многоугольники:
Исходя из
Пошаговое объяснение:
Количество построить k-угольник по 101 точке -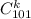 .
.
Тогда количество построить все многоугольники:
Исходя из