Начертите на координатной плоскости (–4;7) (–5;–4) (5;–4) (12;0) (0;3)
(–6;5) (–6;–4) (5;–5) (10;0) (–1;2)
(–6;4) (–7;–5) (4;–5) (10;–1) (–4;2)
(–7;3) (–3;–6) (3;–4) (8;1) (–5;3)
(–7;2) (-6;-6) (2;–4) (6;2) (–5;4)
(–6;1) (–1;–5) (1;–5) (4;2) (–4;6)
(–5;1) (0;–3) (2;-6) (0;5) (–4;7)
(–4;0) (2;–2) (7;–6) (–1;7) (–1;7).
(–3;–3) (3;–3) (10;–2) (–1;6) Глаз:
(–4;–5) (4;–3) (12;–2) (0;4) (–5;4).​

х и у - взаимно простые числа

a = 24 - коэффициент при переменной х

b = 36 - коэффициент при переменной у

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

24 | 2                                      36 | 2

12 | 2                                       18 | 2

6 | 2                                        9 | 3

3 | 3                                        3 | 3

1                                              1

24 = 2³ · 3                              36 = 2² · 3²

НОД(a; b) = 2² · 3 = 12 - наибольший общий делитель

24х : 12 = 2х

36у : 12 = 3у

ответ: НОД (a; b) = 12.

Среднее арифметическое этих восьми чисел будет равно 5,35.

Пошаговое объяснение:

У Вас неполный вопрос, но как я понял, требуется найти среднее арифметическое этих восьми чисел.

Для начала вспомним, что такое среднее арифметическое нескольких чисел: чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество, то есть наглядно это выглядит так:

Для наших трёх чисел это выглядит так: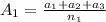

Поэтому по формуле выше мы можем вычислить сумму первых трех чисел, зная что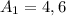 , а :

.

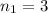Теперь по формуле среднего арифметического, найдем сумму других пяти чисел: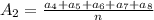

Зная, что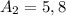 а 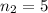, посчитаем сумму этих пяти чисел:

.

Теперь чтобы найти среднее арифметическое всех восьми чисел, требуется сложить сумму первых трех чисел и оставшихся пяти,и поделить на :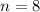

Получили ответ: что среднее арифметическое этих восьми чисел будет равно 5,35.