Над написанием одной программы 6 программистов с одинаковой производительностью работают 10 часов. если 6 программистов начнут работать в 11: 00, и, начиная с 17: 00, к ним каждый час будет присоединяться по одному программисту, то когда работа будет закончена?

Показать ответ

Ответ:

TPROfesorT

17.06.2020 23:56

По традиции примем объем задания за 1.

Т.к. 6 программистов совместно делают работу за 10 ч, то за 1 час эти 6 чел. выполнят 1/10 задания. Тогда 1 чел. за 1 ч выполняет 1/60 задания. С 11⁰⁰ до 17⁰⁰ , т.е. за 6 ч будет выполнено шестью человеками 6/10 = 3/5 задания. Тогда остаток задания составит 1-3/5=2/5.

Поскольку, начиная с 17⁰⁰ к шести человекам каждый час будет добавляться по одному, то доли выпоненного ими задания образуют арифметическую прогрессию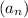 (a_n) , сумма членов которой равна 2/5. Наша задача - определить количесвто n членов прогрессии.

За час работы с 17⁰⁰ до 18⁰⁰ будет выполнено уже семью человеками 7/60 работы, а с 18⁰⁰ до 19⁰⁰ будет выполнено уже восмью человеками 8/60 работы, и т.д.

Поэтому в нашей прогрессии:

$a_1=\frac{7}{60}, \ a_2=\frac{8}{60}, ... , \ S_n=\frac{2}{5} \\\ d=a_2-a_1=\frac{1}{10} \\\ a_n=a_1+d(n-1)=\frac{7}{60}+\frac{1}{60}(n-1)=\frac{1}{10}+\frac{1}{60}n \\\ S_n=\frac{a_1+a_n}{2}n=\frac{\frac{7}{60}+\frac{1}{10}+\frac{1}{60}n}{2}n=\frac{\frac{13}{60}+\frac{1}{60}n}{2}n \\\ \frac{\frac{13}{60}+\frac{1}{60}n}{2}n=\frac{2}{5} \\\ (\frac{13}{60}+\frac{1}{60}n)n=\frac{4}{5} \\\ n^2+13n-48=0 \\\ n_1=-16, \ n_2=3$

По смыслу задачи n=-16 не удовлетворяет условию.

Значит, n=3 - число работников, добавившихся к шести программистам ежечасно, начиная с 17⁰⁰. Тогда на всю работу эли люди потратят 6+3=9 часов, и работа будет закончена в 20⁰⁰.

ответ: в 20⁰⁰.

0,0(0 оценок)

Популярные вопросы: Математика