Пошаговое объяснение:
1)
2)
3)
для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:
теперь чтобы найти обратную матрицу, преобразуем левую часть полученной матрицы в единичную.
1-ую строку делим на -3
1 строку * 5 к 2ой добавляем 1 строку
2-ую строку делим на
и последнее 2ую * (2/3) и к 1 строке добавляем 2ую
и вот
4)
определитель матрицы А:
∆A = 1*1 - 2*1 = -1
nак как A невырожденная матрица, то существует обратная матрица A⁻¹
Умножим справа обе части уравнения на A⁻¹: X·A·A⁻¹ = B·A-1, откуда находим, что X = B·A⁻¹
найдем обратную матрицу A⁻¹.
транспонированная матрица
aлгебраические дополнения
A₁₁ = (-1)¹⁺¹ *1 = 1; A₁₂ = (-1)¹⁺² *1 = -1;
A₂₁ = (-1)²⁺¹ *2 = -2; A₂₂ = (-1)²⁺² *1 = 1;
обратная матрица
тогда
Держи。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆
Пошаговое объяснение:
1)
2)
3)
для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:
теперь чтобы найти обратную матрицу, преобразуем левую часть полученной матрицы в единичную.
1-ую строку делим на -3
1 строку * 5 к 2ой добавляем 1 строку
2-ую строку делим на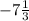
и последнее 2ую * (2/3) и к 1 строке добавляем 2ую
и вот
4)
определитель матрицы А:
∆A = 1*1 - 2*1 = -1
nак как A невырожденная матрица, то существует обратная матрица A⁻¹
Умножим справа обе части уравнения на A⁻¹: X·A·A⁻¹ = B·A-1, откуда находим, что X = B·A⁻¹
найдем обратную матрицу A⁻¹.
транспонированная матрица
aлгебраические дополнения
A₁₁ = (-1)¹⁺¹ *1 = 1; A₁₂ = (-1)¹⁺² *1 = -1;
A₂₁ = (-1)²⁺¹ *2 = -2; A₂₂ = (-1)²⁺² *1 = 1;
обратная матрица
тогда
Держи。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆。・:*:・゚’☆