В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Пошаговое объяснение:
Точка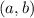
на комплексной плоскости изображает число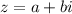 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа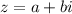
будет являться число 
.
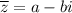В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси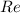
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Для того, чтобы найти координаты точки пересечения графиков функций y = 1.5x и 2y + 2x = 27, необходимо решить систему уравнений:
y = 1.5x;
2y + 2x = 27.
Решения данной системы уравнений и будет координатами точки пересечения графиков данных функций.
Решаем данную систему уравнений.
Подставляя во второе уравнение значение y = 1.5x из первого уравнения, получаем:
2 * 1.5x + 2x = 27;
3х + 2х = 27;
5х = 27;
х = 27 / 5;
х = 5.4.
Зная х, находим у:
y = 1.5x = 1.5 * 5.4 = 8.1.
ответ: координаты точки пересечения графиков данных функций (5.4; 8.1).
Пошаговое объяснение: