Найдите наибольшее целое число являющееся решением неравенства задача 1000​

натуральные числа, целые n >=1

обозначим числа на первой карточке n₁₁ и n₁₂, на второй n₂₁  n₂₂, на третьей n₃₁ n₃₂ и на четвертой n₄₁  n₄₂

Тогда произведение четверок это числа от n₁₁*n₂₁*n₃₁*n₄₁ до n₁₂*n₂₂*n₃₂*n₄₂ а их  сумма равна n₁₁*n₂₁*n₃₁*n₄₁ + n₁₂*n₂₁*n₃₁*n₄₁ + + n₁₂*n₂₂*n₃₂*n₄₁ + n₁₂*n₂₂*n₃₂*n₄₂ = = (n₁₁ + n₁₂)(n₂₁ + n₂₂)(n₃₁ + n₃₂)(n₄₁ + n₄₂)

заметим что n₁₁ + n₁₂ >=2 n₂₁ + n₂₂ >=2 n₃₁ + n₃₂>=2 n₄₁ + n₄₂>=2

по условию (n₁₁ + n₁₂)(n₂₁ + n₂₂)(n₃₁ + n₃₂)(n₄₁ + n₄₂) = 330 = 2*3*5*11 (это произведение сумм с обоих сторон карточек) только одно разложение на 4 простых множителя

значит сумма равна 2+3+5+11 = 21

ответ:  180.  

Вот формула площади трапеции:

, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).

Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен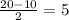 . Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:  

Теперь высоту мы знаем и можем найти площадь трапеции:

Задача решена!