Задание. Найдите наибольшее целое решение неравенства:
Решение. Выпишем ограничения логарифмов:
По свойству логарифма имеем:
По свойству степеней имеем:
Поскольку основание логарифма при переходе к подлогарифмическим выражениям знак неравенства должен изменится на противоположный:
Неравенство вида равносильно
Имеем:
Учитывая ограничения получаем решение:
Наибольшим целым решением данного неравенства является число 0.
ответ: 0.
Задание. Найдите наибольшее целое решение неравенства:
Решение. Выпишем ограничения логарифмов:
По свойству логарифма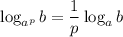 имеем:
имеем:
По свойству логарифма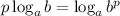 имеем:
имеем:
По свойству степеней![a^{\tfrac{m}{n} } = \sqrt[n]{a^{m}}](/tpl/images/4514/7512/f52d1.png) имеем:
имеем:
Поскольку основание логарифма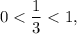 при переходе к подлогарифмическим выражениям знак неравенства должен изменится на противоположный:
при переходе к подлогарифмическим выражениям знак неравенства должен изменится на противоположный:
Неравенство вида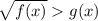 равносильно
равносильно 
Имеем:
Учитывая ограничения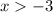 получаем решение:
получаем решение: 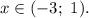
Наибольшим целым решением данного неравенства является число 0.
ответ: 0.