Так как log_4(x) - монотонно возрастающая функция, то наименьшее значение ymin функция y=log_4(x²-6*x+17) принимает при наименьшем значении выражения x²-6*x+17. А так как x²-6*x+17=(x-3)²+8, то отсюда следует, что наименьшее значение этого выражения равно 8 и тогда ymin=log_4(8)=1,5
ответ: 1,5.
Пошаговое объяснение:
Так как log_4(x) - монотонно возрастающая функция, то наименьшее значение ymin функция y=log_4(x²-6*x+17) принимает при наименьшем значении выражения x²-6*x+17. А так как x²-6*x+17=(x-3)²+8, то отсюда следует, что наименьшее значение этого выражения равно 8 и тогда ymin=log_4(8)=1,5
ответ: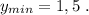
Пошаговое объяснение: