Найдите последнюю ненулевую цифру произведения всех натуральных чисел от 1 до 40

Показать ответ

Ответ:

ksyhaua0406ozoo6s

18.11.2022 08:27

Условие задачи некорректно.

Пошаговое объяснение:

Пусть в книге х страниц. В первый день Азамат прочел 0,25х всей книги. Во второй день ему остается х-0,25х= 0,75х от всей книги. 40% от всего оставшегося будет равно 0,4*0,75х=0,3х - книги Азамат прочитал во второй день. В третий день ему остается х-0,25х-0,3х=х-0,55х=0,45х всей книги. Получается, что

в первый день Азамат прочел 0,25х всей книги,

во второй день Азамат прочел 0,3х от всей книги,

в третий день Азамат прочел 0,45х всей книги.

Получается, что в третий день Азамат прочел больше, чем во второй. Но в условии задачи говорится, что во второй день Азамат прочитал на 18 страниц больше. Значит условие задачи некорректно.

0,0(0 оценок)

Ответ:

vedernikowadia

07.03.2020 12:54

4. Из основного тригонометрического тождества:

$\sin^2\alpha + \cos^2\alpha = 1\\\\\sin^2\alpha = 1 - \cos^2\alpha\\\\\sin\alpha = \sqrt{1 - \cos^2\alpha}$

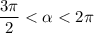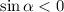Так как $\dfrac{3\pi}{2} < \alpha < 2\pi$ , то $\sin\alpha < 0$ .

$\sin\alpha = -\sqrt{1-\cos^2\alpha} = -\sqrt{1-0,8^2} = -\sqrt{1-0,64} = -\sqrt{0,36} = \bf{-0,6}$ .

ответ: -0,6

$\sqrt[6]{\left(m-n\right)^6} - \sqrt[4]{m^4} = \left|m-n\right| - \left|m\right|$

Так как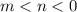 , то модуль будет раскрываться вот так:

$\left|m-n\right| - \left|m\right| = -(m-n) -(-m) = n - m + m = \bf{n}$

ответ: n

6. (см. чертёж во вложении) Сечение шара представляет собой круг. Площадь круга задаётся формулой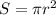 $S = \pi r^2$ , отсюда:

$\pi r^2 = 9\pi\\\\r^2 = 9\\\\r = 3$

Получается прямоугольный треугольник, где гипотенуза - это радиус шара, один катет - радиус сечения, второй катет - расстояние от центра шара до сечения. По теореме Пифагора:

$R^2 = r^2 + h^2\\\\R = \sqrt{r^2+h^2} = \sqrt{9+16} = \sqrt{25} = 5$

Формула объёма шара: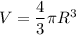 $V = \dfrac{4}{3}\pi R^3$ . Подставляем известные значения:

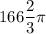
$V = \dfrac{4}{3} \cdot \pi\cdot 125 = \dfrac{500\pi}{3} = \bf166\dfrac{2}{3} \pi$

ответ: $166\dfrac{2}{3}\pi$

$4^{-(1-x)^2} \leqslant 0,5^{3x+2}\\\\\left(2^2\right)^{-(1-x)^2}\leqslant \left(2^{-1}\right)^{3x+2}\\\\2^{-2(1-x)^2} \leqslant 2^{-3x-2}\\\\2^{-2(1-2x+x^2)} \leqslant 2^{-3x-2}\\\\2^{-2+4x-2x^2}\leqslant 2^{-3x-2}\\\\-2+4x-2x^2\leqslant-3x-2\\\\2x^2 - 7x \geqslant 0\\\\x(2x - 7)\geqslant 0$