Пошаговое объяснение:
Нужно взять производную сначала от арксинуса.
Это будет
Теперь возьмем производную от логарифма. Получим
Осталось взять производную от выражения под логарифмом.
Это будет 2.
Теперь все это нужно перемножить по правилам взятия производной от сложной функции.
Это и будет искомой производной.
y=arcsin(ln(2x))
(arcsinx)'=1/√(1-x²) ⇒
y'=arcsin(ln(2x)'=(1/√(1-ln²(2x))*(ln(2x))'*(2x)'=
=(1/√(1-ln²(2x))*(1/(2x))*2=1/(x*√(1-ln²(2x)).
Пошаговое объяснение:
Нужно взять производную сначала от арксинуса.
Это будет
Теперь возьмем производную от логарифма. Получим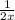
Осталось взять производную от выражения под логарифмом.
Это будет 2.
Теперь все это нужно перемножить по правилам взятия производной от сложной функции.
Это и будет искомой производной.
Пошаговое объяснение:
y=arcsin(ln(2x))
(arcsinx)'=1/√(1-x²) ⇒
y'=arcsin(ln(2x)'=(1/√(1-ln²(2x))*(ln(2x))'*(2x)'=
=(1/√(1-ln²(2x))*(1/(2x))*2=1/(x*√(1-ln²(2x)).