Найти длину окружности если радиус равен - 100 метров а соответствующий центральный угол *а) б) и в)

запишите суммы в десятичной системе счисления

3*1000+2*100+4*10+5= 3245.

1)) 3•1000=3000

2)) 2•100=200

3)) 4•10=40

4)) 3000+ 200+ 40+ 5= 3245

запишите суммы с римских цифр

III • M+ II • C+ IV • X= MMMCCXLV.

1)) III•M=MMM

2)) II•C=CC

3))IV•X=XL

4)) MMM+ CC+XL+V=MMMCCXLV

1=I;

5=V;

10=X

50=L

100=C

500=D

1000=M

Пошаговое объяснение:

Числа записываем так; если меньшее число впереди (слева) до пяти и в десятках до 50, в сотнях до 500; все надо вычитать; если после них (справа), то прибавлять.

например

14, это 10+ 5-1; пишем 10, X, вперёд неё пишем 5, V и ещё вперёд 1, I; получили IVX; или 9, это 10-1; пишем Х, вперёд 1, I, 9= IX;

или

Пошаговое объяснение:

Нам нужно составить уравнение геометрического места точек на плоскости ОXY равноудаленных от точек с координатами A (2; -3) и B (-4; 1).

Решать задачу будем следующим образом:

 вспомним формулу для нахождения расстояния между точками на плоскости;

 обозначим точки равноудаленные от А и В координатами (x; y);

 запишем расстояния между точкой А и (x; y);

 запишем расстояние между точками B и (x; y);

 приравняем расстояния и выразим одну переменную через другую.

Вспомним формулу для нахождения расстояния на плоскости

Формула для нахождения расстояния между точками на плоскости выглядит так:

AB =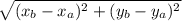 , где точки А и В заданы координатами A  и B

Формулу мы вспомнили, теперь можем записать расстояние между точками А с координатами (2; -3) и (x; y) и точками B с координатами (-4; 1) и (x; y).

Составим уравнение геометрического места точек

Записываем расстояние между точкой A (2; -3) и (x; y):

;

Записываем расстояние между точками B (-4; 1) и (x; y):

;

Так как геометрического места точек на плоскости ОXY равноудаленных от точек A и B мы приравниваем полученные выражения:

;

;

Открываем скобки, переносим все слагаемые в право и приводим подобные.

;

или  

.