ответ: y = sinx + Ccosx
Пошаговое объяснение:
Домножим левую и правую части уравнения на комплектующий множитель :
Заметим, что
Воспользуемся тем, что левая часть последнего диф. уравнения это дифференциал произведения двух функций.
ответ: y = sinx + Ccosx
Пошаговое объяснение:
Домножим левую и правую части уравнения на комплектующий множитель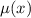 :
:
Заметим, что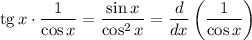
Воспользуемся тем, что левая часть последнего диф. уравнения это дифференциал произведения двух функций.