Метод Эйлера.
Решениями являются следующие пары:
Причем по условию .
Для вычисления используется формула:
, где
В дальнейших вычислениях результат будем округлять до тысячных:
Итак, приближенные решения:
Метод Рунге-Кутта:
Аналогично, последующие значения вычисляются через предыдущие, только по другой формуле:
, где:
Рассчитаем :
Результаты остальных расчетов показаны в таблице.
Приближенные решения:
Метод Эйлера.
Решениями являются следующие пары:
Причем по условию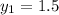 .
.
Для вычисления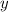 используется формула:
используется формула:
В дальнейших вычислениях результат будем округлять до тысячных:
Итак, приближенные решения:
Метод Рунге-Кутта:
Аналогично, последующие значения вычисляются через предыдущие, только по другой формуле:
Рассчитаем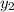 :
:
Результаты остальных расчетов показаны в таблице.
Приближенные решения: