Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
А
Английский язык
Х
Химия
Э
Экономика
П
Право
И
Информатика
У
Українська мова
Қ
Қазақ тiлi
О
ОБЖ
Н
Немецкий язык
Б
Беларуская мова
У
Українська література
М
Музыка
П
Психология
А
Алгебра
Л
Литература
Б
Биология
М
МХК
О
Окружающий мир
О
Обществознание
И
История
Г
Геометрия
Ф
Французский язык
Ф
Физика
Д
Другие предметы
Р
Русский язык
Г
География
Показать больше
Показать меньше
ЯМС
29.01.2023 07:50 •
Математика
Найти производные первого порядка данных функций у= 3x^5– sinx ,
2) у=корень (Х) tgx
3) y=lnx/4-3cosx
4) y= под общей скобкой { x=arcsin 2t,
{ y=1/1-4t^2
Подробное решение
Показать ответ
Ответ:
ivan19852008
13.02.2021 23:22
Пошаговое объяснение:
1)
2)
3)
4)
0,0
(0 оценок)
Популярные вопросы: Математика
Understand11
25.09.2021 01:09
Маша выехали в школу на самокате со скоростью 200 м в минуту через 7 минут вслед за ней из школы выехала и её одноклассница Настя на скейте со скоростью 340 метров в...
polyakovred
24.12.2021 23:02
Розв яжiть рiвняння - (4х-3)=-7х ХЕЛП...
silonte
07.12.2020 17:14
Никита пришёл в парк аттракционов в 11 ч 25 минут, а ушёл из парка днём, в половине второго. Сколько минут пробыл в парке аттракционов Никита?...
TheSiDo
05.12.2022 05:42
В высотном доме 3 лифта. Для каждого лифта вероятность того, что он находится на первом этаже, равна 0,5 . Найдите вероятность того, что ровно два лифта находятся на...
tanyatomeva81
09.03.2023 03:00
Начертите прямоугольник длиной 15 mm ишириной 10 mm. Найдите его площадь,ОТІП тетради начертите квадрат...
Shofer123
17.07.2022 17:55
Боковые стороны прямоугольной трапеции равны 6см и 7.5см, меньшее основание равно 8см, а перпендикулярная боковой стороне диагональ-10см. Найдите площадь и большее основание...
VaLeRiA102030405060
08.06.2022 05:48
Исследовать кривую y=1/3x^3*2x^2-1/3 на экстремум и точки перегиба.Построить схематический график этой функции...
pomorcevakata98
28.09.2020 04:56
В музее в 5 залах по 29 картин в каждом и 3 зала - по 37 картин в каждом. Сколько всего картин в этих залах?...
aleksandrdream4
27.11.2021 05:06
100 б. Отмечаю лучшим✌...
Нюша1390
06.09.2021 23:07
Что больше и на сколько ; сумма всех чётных чисел от 1 до 10 или сумма всех нечётных чисел от 1 до 10?...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Пошаговое объяснение:
1)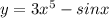
2)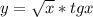
3)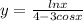
4)