Пошаговое объяснение:
умножим обе части на х
теперь при у заменим 1 на dx/dx
⇒
теперь проинтегрируем обе части по х
откуда и получим
теперь условие
y(1) = 1 ⇒ ⇒ C = 0
и вот решение задачи Коши
y(x) = x²
Пошаговое объяснение:
умножим обе части на х
теперь при у заменим 1 на dx/dx
теперь проинтегрируем обе части по х
откуда и получим
теперь условие
y(1) = 1 ⇒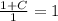
⇒ C = 0
и вот решение задачи Коши
y(x) = x²