Найти уравнение плоскости, проходящей через точки
K(4, 1, −3), L(5, −2, −2), M(6, 5, −7).

Тут мы должны учесть некоторое обстоятельство. В ящике шаров желтых 2, а мы должны вытащить четыре. Мы не можем этого сделать. Вероятность 0. Однако, я рассмотрю вероятность всех шаров, может в условии ошибка. Рассмотрим вероятность вытаскивания черного шара. Вероятность - число, равное отношению благоприятных событий к общему их количеству. Итак, вероятность для черных равна. 12\(12+7+2)=12\21. Вероятность вытаскивания желтого шара равна 2\21. Казалось, формула (((Вероятность вытаскивания черного шара)^(кол-во черных))*((Вероятность вытаскивания желтого шара)^(кол-во желтых))=ответ) работает. Но увы.

ответ: 0

Подробнее - на -

Пошаговое объяснение:

Пошаговое объяснение:

Точка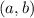 на комплексной плоскости изображает число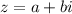

- действительная часть числа (Real)

- мнимая часть числа (Imaginary)

В соответствии с этим строим точки для 16.1. (Картинка 1)

Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.

Т.е. сопряженным для числа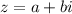 будет являться число .

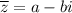В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).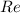

На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.