Дан полушар с радиусом R = OC и описанный около него конус с радиусом основания r = OA и высотой h = OM.
Построим сечение конуса по диаметру основания : ΔAMB
OM - высота конуса ⇒ ΔAMO - прямоугольный. Пусть ∠OMK=α
OK⊥AM - как радиус шара в точку касания с конусом ⇒ ΔOKM - прямоугольный. По отношению сторон прямоугольного треугольника :
По отношению сторон прямоугольного треугольника ΔAMO:
Тогда объём конуса по формуле
Объём конуса, выраженный дробью, будет наименьшим, когда знаменатель будет наибольшим.
Наибольшее значение функции в знаменателе можно найти через производную.
f (α) = sin α - sin³ α
f'(α) = (sin α - sin³ α)' = 0
cos α - 3 sin² α cos α = 0
cos α (1 - 3 sin²α) = 0
1) cos α = 0 ⇒ α = 90° - не подходит по условию (угол при вершине сечения не может быть равен 180°).
1 - 3 sin²α = 0 ⇒ ⇒
- только положительное значение корня, так как отрицательным угол при вершине конуса быть не может.
Высота конуса
ответ:
=======================================
Наименьший объём описанного конуса с высотой h=√3 R
Дан полушар с радиусом R = OC и описанный около него конус с радиусом основания r = OA и высотой h = OM.
Построим сечение конуса по диаметру основания : ΔAMB
OM - высота конуса ⇒ ΔAMO - прямоугольный. Пусть ∠OMK=α
OK⊥AM - как радиус шара в точку касания с конусом ⇒ ΔOKM - прямоугольный. По отношению сторон прямоугольного треугольника :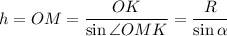
По отношению сторон прямоугольного треугольника ΔAMO:
Тогда объём конуса по формуле
Объём конуса, выраженный дробью, будет наименьшим, когда знаменатель будет наибольшим.
Наибольшее значение функции в знаменателе можно найти через производную.
f (α) = sin α - sin³ α
f'(α) = (sin α - sin³ α)' = 0
cos α - 3 sin² α cos α = 0
cos α (1 - 3 sin²α) = 0
1) cos α = 0 ⇒ α = 90° - не подходит по условию (угол при вершине сечения не может быть равен 180°).
1 - 3 sin²α = 0 ⇒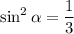 ⇒
⇒
Высота конуса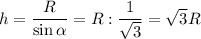
ответ: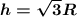
=======================================
Наименьший объём описанного конуса с высотой h=√3 R