Математика: Номер 847 Найдите корни уравнений

Номер 847 Найдите корни уравнений

Показать ответ

Ответ:

Frosterion

17.10.2022 01:46

На циферблате имеется 60 делений, на которые приходится 360 градусов. Значит, когда стрелка пройдёт 1 деление, то она переместиться на   360:60=6 градусов.
Минутная стрелка за 15 мин пройдёт 6*15=90 градусов.
Определим, сколько делений пройдёт часовая стрелка за то время, пока мин. стрелка проходит 15 минут, зная, что часовая стрелка проходит 5 делений за 1 час, то есть за то время, за которое минутная стрелка проходит 60 делений.
5 делений   - 1 час (60 мин)
х делений   -  15 минут              х=5*15:60=1,25 (делений)
Теперь определим, на сколько градусов повернётся часовая стрелка, пока минутная поворачивается на 90 градусов (то есть минутная проходит 15 минут):
     1 деление - 6 градусов
1,25 делений - х градусов      х=1,25*6:1=7,5 (градусов)
Угол между минутной и часовой стрелками составляет
90-7,5=82,5 градусов=82 градуса 30 минут

0,0(0 оценок)

Ответ:

temayurin2016

06.12.2022 03:04

Найдите все значения а, при каждом из которых неравенство |x²-4x+a-5| ≤ 10 выполняется для всех x∈[a-5;a].

-10 ≤ x²-4x+a-5 ≤ 10

-x²+4x+5-10 ≤ a ≤ -x²+4x+5+1

-(x-2)²-1 ≤ a ≤ -(x-2)²+19 (1)

В декартовой системе координат а от х построим ГМТ удовлетворяющих неравенству (1). Эта область заключена между двумя параболами a = -(x-2)²-1 и a = -(x-2)²+19, включая сами параболы.

По условию a-5 ≤ x ≤ a, преобразуем:

$\displaystyle \left \{ {{a-5\le x} \atop {a\ge x}} \right. \quad \left \{ {{a\le x+5} \atop {a\ge x}} \right.\\\\ x\le a\le x+5\quad (2)$

Неравенство (2) задаёт область, которая ограничена двумя параллельными прямыми a=x-5 и a=x, включая границы.

Определим как взаимно расположены эти области.

$\displaystyle \left \{ {{a=x\qquad \qquad \quad } \atop {a=-x^2+4x-5}} \right. \quad \left \{ {{a=x\qquad \qquad \qquad } \atop {-x^2+4x-5-x=0}} \right. \\\\-\left( x-\dfrac32 \right) ^2-2\dfrac34 =0;\quad x\in \varnothing$

Прямая a=x не имеет общих точек с нижней границей графика (1), значит и прямая a=x+5 не имеет с ней общих точек.

$\displaystyle \left \{ {{a=x+5\qquad \qquad } \atop {a=-x^2+4x+15}} \right. \quad \left \{ {{x=a-5\qquad \qquad \qquad \qquad \quad } \atop {a+(a-5)^2-4(a-5)-15=0}} \right. \\\\a^2-13a+30=0;\quad D_1=169-120=7^2\\a=\dfrac{13\pm 7}2 =\{3;10\}$

Прямая a=x+5 пересекает верхнею границу графика (1) в двух различных точках с ординатами 3 и 10. Значит и прямая а=х пересекает эту границу, надём ординаты общих точек.

$\displaystyle \left \{ {{a=x\qquad \qquad \quad } \atop {a=-x^2+4x+15}} \right. \quad \left \{ {{a=x\qquad \qquad \qquad } \atop {a+a^2-4a-15=0}} \right. \\\\a^2-3a-15=0;\quad D_2=9+60=69\\a=\dfrac{3\pm \sqrt{69}}2$

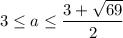
При фиксированном a, все точки (x;a) графика (2) должны находится в области графика (1). По графику видно, что подходят только $3\le a\le \dfrac{3+\sqrt{69}}2$