Обозначим x % и y % - процентные содержания меди в первом и во втором сплавах соответственно и рассмотрим рисунки 3 и 4.
1 кг 2 кг
Медь
x % Цинк + Медь
y % Цинк
3 кг
= Медь
50% Цинк
Рис. 3
На рисунке 3 изображена структура сплава, состоящего из 1 килограмма первого сплава и 2 килограммов второго сплава. Масса этого сплава – 3 килограмма.
4 кг 1 кг
Медь
x % Цинк + Медь
y % Цинк
5 кг
= Медь
36% Цинк
Рис.4
На рисунке 4 изображена структура сплава, состоящего из 4 килограммов первого сплава и 1 килограмма второго сплава. Масса этого сплава – 5 килограммов.
Записывая баланс меди в сплаве, структура которого изображена на рисунке 3, а также баланс меди в сплаве, структура которого изображена на рисунке 4, получим систему из двух уравнений с двумя неизвестными x и y :
задачи на смеси задачи на сплавы задачи на растворы концентрация процентная концентрация процентное содержание массовая концентрация объемная концентрация примеры решения задач
Далее получаем
задачи на смеси задачи на сплавы задачи на растворы концентрация процентная концентрация процентное содержание массовая концентрация объемная концентрация примеры решения задач
ответ. В первом сплаве содержание меди 30% , во втором сплаве содержание меди 60% .
Вы не поставили знаки возведения в степень (не забывайте их, иначе выражение совсем непонятно- приходится гадать, что за действие там было- умножение или возведение в степень).
Вот это выражение со знаками возведения в степень:
(x^2 - 6x + 9) + (5y - 3)^2 + (4z + 5)^4 = 0
А записав это же в поле уравнение (кнопка ), получим как на бумаге:
Решаем:
Отсюда получаем, что все три слагаемых должны быть равны нулю:
Считаем заданное выражение:
ответ: вариант 4
Задание 2
В тексте задачи опечатка- сравнивается время второго пешехода со вторым же. Если предположить, что правильный текст такой: "За сколько времени первый расстояние АВ", то имеем вот что:
Обозначим величины:
S - расстояние от A до B
t1 - время в пути первого пешехода
t2 - время в пути второго пешехода
v1 - скорость первого пешехода
v2 - скорость второго пешехода
Считаем что они двигались равномерно (не меняя скорости).
Первый и второй до точки встречи шли 3 часа. За это время они суммарно полное расстояние S. Запишем это, вычисляя путь каждого через его скорость и время (3 ч):
Запишем скорости пешеходов через путь и время каждого и подставим в уравнение выше.
Т.к. , то можем поделить обе части уравнения на :
Выразим время t2 через t1 (они связаны по условиям задачи), и подставим это выражение вместо t2 в уравнение:
Умножим обе части уравнения на :
(при этом нужно указать, что )
(ч)
(ч)
Значение 1 ч не подходит по условиям задачи (оно меньше 3 ч).
А значение 7,5 ч - подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или 2,5), но отсутствует среди вариантов ответа (если только вы первый вариант не записали с очередной ошибкой- 7 вместо 7,5).
То есть, в таком виде задачи, ответ будет- нет верных вариантов.
Решение будет подходить под эти варианты, только если предположить, что в тексте задачи вообще всё перепутано, и правильный текст на самом деле звучит как то так:
"Два пешехода вышли одновременно навстречу друг другу – первый из пункта А, второй из пункта В. Они встретились через три часа. За сколько времени первый расстояние АВ, если он пришёл в пункт В на 2,5 часа раньше, чем второй пришёл в пункт А."
В этом случае получим такое решение:
Т.к. , то можем поделить обе части уравнения на :
Умножим обе части уравнения на :
(при этом нужно указать, что )
(ч)
(ч)
Значение -1,5 ч не подходит по условиям задачи (здесь отрицательное время не имеет смысла).
Значение 5 ч -подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или -2,5) и присутствует среди вариантов ответа.
ответ: вариант 3
ВЫВОД: сверьте текст задания с исходным- если при наборе действительно были допущены указанные мной ошибки, то вариант решения я привёл выше (и, в следующий раз проверяйте текст перед отправкой задания).
Обозначим x % и y % - процентные содержания меди в первом и во втором сплавах соответственно и рассмотрим рисунки 3 и 4.
1 кг 2 кг
Медь
x % Цинк + Медь
y % Цинк
3 кг
= Медь
50% Цинк
Рис. 3
На рисунке 3 изображена структура сплава, состоящего из 1 килограмма первого сплава и 2 килограммов второго сплава. Масса этого сплава – 3 килограмма.
4 кг 1 кг
Медь
x % Цинк + Медь
y % Цинк
5 кг
= Медь
36% Цинк
Рис.4
На рисунке 4 изображена структура сплава, состоящего из 4 килограммов первого сплава и 1 килограмма второго сплава. Масса этого сплава – 5 килограммов.
Записывая баланс меди в сплаве, структура которого изображена на рисунке 3, а также баланс меди в сплаве, структура которого изображена на рисунке 4, получим систему из двух уравнений с двумя неизвестными x и y :
задачи на смеси задачи на сплавы задачи на растворы концентрация процентная концентрация процентное содержание массовая концентрация объемная концентрация примеры решения задач
Далее получаем
задачи на смеси задачи на сплавы задачи на растворы концентрация процентная концентрация процентное содержание массовая концентрация объемная концентрация примеры решения задач
ответ. В первом сплаве содержание меди 30% , во втором сплаве содержание меди 60% .
Задание 1
Вы не поставили знаки возведения в степень (не забывайте их, иначе выражение совсем непонятно- приходится гадать, что за действие там было- умножение или возведение в степень).
Вот это выражение со знаками возведения в степень:
(x^2 - 6x + 9) + (5y - 3)^2 + (4z + 5)^4 = 0
А записав это же в поле уравнение (кнопка ), получим как на бумаге:
), получим как на бумаге:
Решаем:
Отсюда получаем, что все три слагаемых должны быть равны нулю:
Считаем заданное выражение:
ответ: вариант 4
Задание 2
В тексте задачи опечатка- сравнивается время второго пешехода со вторым же. Если предположить, что правильный текст такой: "За сколько времени первый расстояние АВ", то имеем вот что:
Обозначим величины:
S - расстояние от A до B
t1 - время в пути первого пешехода
t2 - время в пути второго пешехода
v1 - скорость первого пешехода
v2 - скорость второго пешехода
Считаем что они двигались равномерно (не меняя скорости).
Первый и второй до точки встречи шли 3 часа. За это время они суммарно полное расстояние S. Запишем это, вычисляя путь каждого через его скорость и время (3 ч):
Запишем скорости пешеходов через путь и время каждого и подставим в уравнение выше.
Т.к.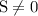 , то можем поделить обе части уравнения на
, то можем поделить обе части уравнения на 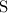 :
:
Выразим время t2 через t1 (они связаны по условиям задачи), и подставим это выражение вместо t2 в уравнение:
Умножим обе части уравнения на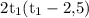 :
:
(при этом нужно указать, что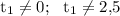 )
)
Значение 1 ч не подходит по условиям задачи (оно меньше 3 ч).
А значение 7,5 ч - подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или 2,5), но отсутствует среди вариантов ответа (если только вы первый вариант не записали с очередной ошибкой- 7 вместо 7,5).
То есть, в таком виде задачи, ответ будет- нет верных вариантов.
Решение будет подходить под эти варианты, только если предположить, что в тексте задачи вообще всё перепутано, и правильный текст на самом деле звучит как то так:
"Два пешехода вышли одновременно навстречу друг другу – первый из пункта А, второй из пункта В. Они встретились через три часа. За сколько времени первый расстояние АВ, если он пришёл в пункт В на 2,5 часа раньше, чем второй пришёл в пункт А."
В этом случае получим такое решение:
Т.к.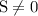 , то можем поделить обе части уравнения на
, то можем поделить обе части уравнения на 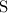 :
:
Умножим обе части уравнения на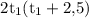 :
:
(при этом нужно указать, что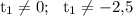 )
)
Значение -1,5 ч не подходит по условиям задачи (здесь отрицательное время не имеет смысла).
Значение 5 ч -подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или -2,5) и присутствует среди вариантов ответа.
ответ: вариант 3
ВЫВОД: сверьте текст задания с исходным- если при наборе действительно были допущены указанные мной ошибки, то вариант решения я привёл выше (и, в следующий раз проверяйте текст перед отправкой задания).