Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=16см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=16см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-16=15см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=15см ⇒ AB=15см.
Число противоположное равно числу, противоположному , то есть . К числу мы прибавляем :
(Противоположное число - число, которое на числовой прямой имеет такое же расстояние от 0, что у данного, но он стоит по другую сторону от 0, например, противоположное число 5 равно -5, так как на числовой прямой у них одинаковое расстояние до 0 (расстояние равно 5), но 5 стоит справа от 0, а противоположное должно стоять по другую сторону, то есть слева, Число, стоящее слева от нуля и имеющее расстояние 5 равно -5).
Вступление
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=16см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=16см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-16=15см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=15см ⇒ AB=15см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 15см.
14
Пошаговое объяснение:
Число противоположное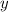
равно числу, противоположному 
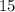, то есть 
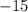. К числу 
мы прибавляем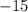 
:
(Противоположное число - число, которое на числовой прямой имеет такое же расстояние от 0, что у данного, но он стоит по другую сторону от 0, например, противоположное число 5 равно -5, так как на числовой прямой у них одинаковое расстояние до 0 (расстояние равно 5), но 5 стоит справа от 0, а противоположное должно стоять по другую сторону, то есть слева, Число, стоящее слева от нуля и имеющее расстояние 5 равно -5).
ответ: 14